Introduction
A wave is a disturbance that travels through space and time, accompanied by a transfer of energy. A wave motion is produced due to harmonic oscillations of a series of points of the medium.
Types of Waves
Mechanical wave
Waves that require a material medium for propagation are called mechanical waves. Here waves are produced by periodic vibrations of the particles of the medium.
Example : Sound waves & Seismic waves
Electromagnetic waves
Waves which does not require a material medium for propagation are called electromagnetic waves. So they can travel through vaccum. In electromagnetic waves, electric & magnetic fields oscillates perpendicular to direction of propagation of wave.
Examples: Light waves, Radio waves, X-rays etc..
According to the direction of vibration of the particles of medium with respect to direction of propagation of waves are classified into two types
Transverse waves.
If the direction of vibration of the particles of medium is perpendicular to direction of propagation of wave, such waves are called transverse waves.
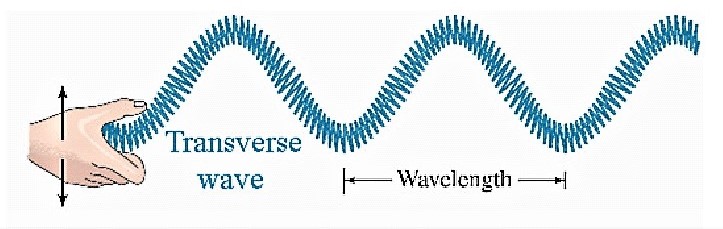
Example : light waves and water waves
Longitudinal waves.
If the direction of vibration of the particles of medium is parallel to direction of propagation of wave, such waves are called longitudinal waves.
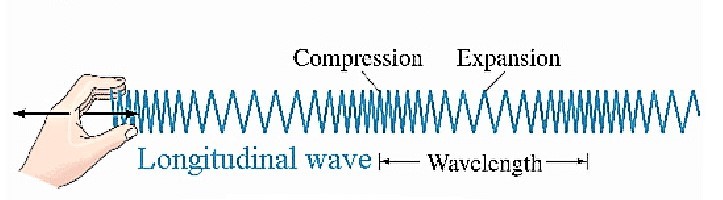
Example : sound waves and ultrasonic waves
Properties of Waves
Wavelength
Wavelength is a measure of the distance between two consecutive peaks (or troughs) of a wave. Generally wavelength can be defined as distance between two consecutive points of a wave that are in phase.

Wave vector (wave number)
A wave vector (also called wave number) is a vector quantity that describes the direction and magnitude of a wave in space. It is typically represented by the symbol k and can be related to wavelength, \( \lambda \) as, $$ \boxed{k=\frac{2 \pi}{\lambda}} $$ The direction of the wave vector indicates the direction of wave propagation.Frequency
Frequency of a wave is the number of oscillations or vibrationsof particles of medium (or wave itself) per unit time.
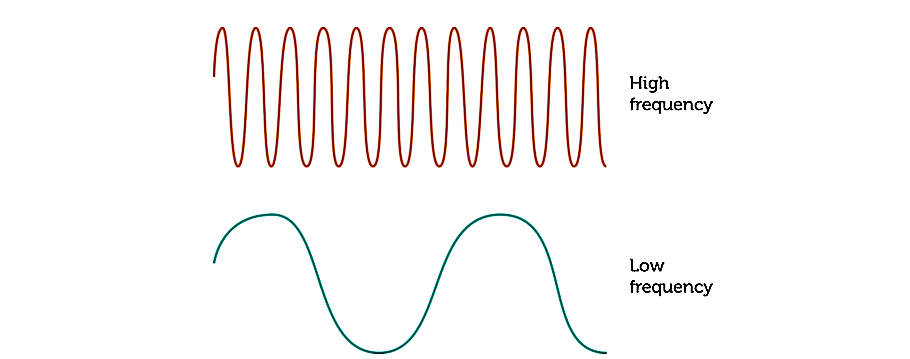
Angular frequency
Angular frequency is a measure of the rate of change of the phase of a wave.It is typically denoted by the Greek letter omega (ω) and has units of radians per second (rad/s). Angular frequency is related to the frequency(f) of a wave, by the equation: $$\boxed{ \omega = 2 \pi f }$$Amplitude
Amplitude is maximum displacement of a particle from equilibrium point in a wave (keep in mind that wave is propagation of vibration/oscillation of this particles in a medium). It is the distance between the highest point (crest) or the lowest point (trough) of a wave and the equilibrium or rest position.
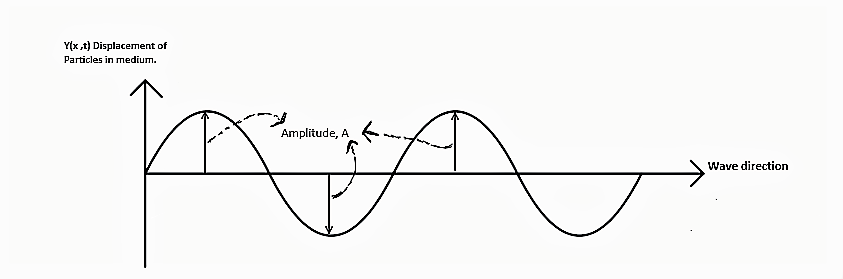
Wave velocity
Wave velocity is a measure of the speed at which a wave travels through a medium and depends on the properties of the medium and the wavelength and frequency of the wave.
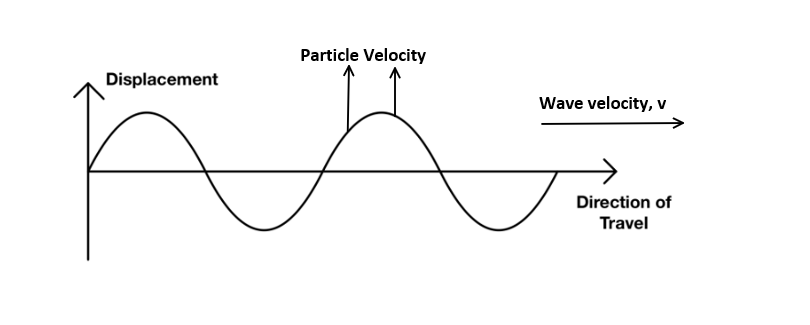
Particle velocity
particle velocity of a wave is the velocity of the individual particles of the medium oscillates. It varies depending on the position in the medium, it's different from the wave velocity which is the speed at which the wave itself travels.
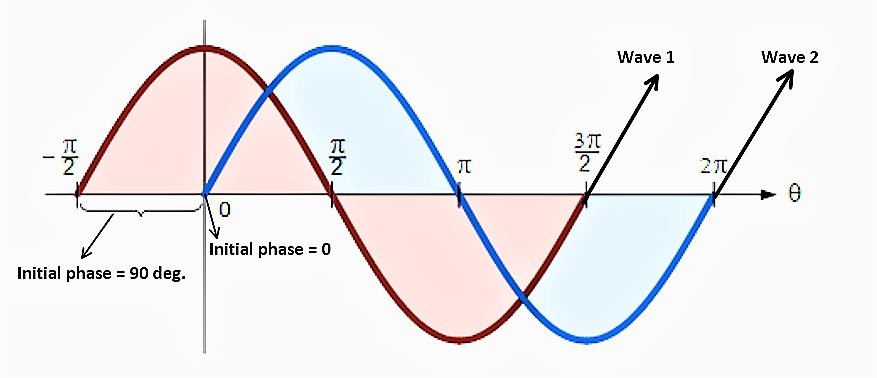
Initial phase
Initial phase of a wave is the starting point or position of a wave cycle at a given time, it's measured in degrees and it gives the position of a point on the waveform in relation to a reference point.
Wave equation
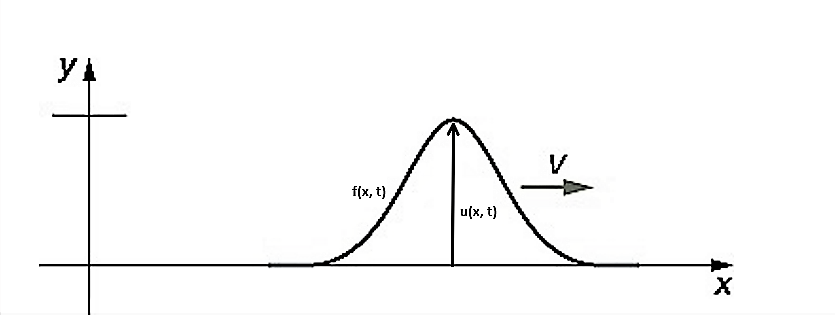
A single pulse or wave moving in positive x direction can be represented as,
$$u(x,t)=f(x-vt)\;-->(eqn1)$$where u is the vertical displacement of particle in wave and f is the function representing shape of the waveform.
Differentiating equation (1) w.r.t to x twice,
$$\frac{\partial^u}{\partial x^2}=f^{''}(x-vt) \; ---eqn(2)$$Differentiating equation (1) w.r.t t twice
$$\frac{\partial^u}{\partial t^2}=v^2 \;f^{''}(x-vt)\;---eqn(3)$$substituting value of \(f^{''}(x-vt)\) from equation(2) in equation(3),
$$\frac{\partial^u}{\partial t^2} =v^2 \; \frac{\partial^u}{\partial x^2} $$rearranging,
$$\boxed{\frac{\partial^2 u}{\partial x^2} =\frac{1}{v^2} \; \frac{\partial^u}{\partial t^2}} $$Above equation is called one dimensional wave equation.
Three Dimensional equation
3-D wave equation is represented as,
$$\frac{\partial^2 u}{\partial x^2}+ \frac{\partial^2 u}{\partial y^2} + \frac{\partial^2 u}{\partial z^2}=\frac{1}{v^2} \; \frac{\partial^u}{\partial t^2} $$ or $$\boxed{ \nabla^2 u =\frac{1}{v^2} \; \frac{\partial^u}{\partial t^2}} $$ where \( \nabla^2 \) is called laplacian operator. $$ \nabla^2 = \frac{\partial^2 }{\partial x^2}+ \frac{\partial^2 }{\partial y^2} + \frac{\partial^2 }{\partial z^2}$$Solution of Wave equation
One dimensional wave equation is given by, $$ \frac{\partial^2 u}{\partial x^2} =\frac{1}{v^2} \; \frac{\partial^u}{\partial t^2} --eqn(1)$$ Assume that solution of above differential equation is given by, $$ u(x,t)=X(x)\;T(t)--eqn(2)$$ where \( X(x)\) is function of x only and \( T(t)\) is the function of t only. Differentiating equation (2) with x and t respectively, $$ \frac{\partial^2 u}{\partial x^2}= T \;\frac{\partial^2 X}{\partial x^2}$$ $$ \frac{\partial^2 u}{\partial t^2}= X \;\frac{\partial^2 T}{\partial t^2}$$ Substituting this expression in equation (1), $$T \;\frac{\partial^2 X}{\partial x^2} = \frac{1}{v^2}\;X \;\frac{\partial^2 T}{\partial t^2}$$ rearranging, $$\frac{1}{X}\;\frac{\partial^2 X}{\partial x^2} = \frac{1}{Tv^2} \;\frac{\partial^2 T}{\partial t^2}$$ Left hand side of above equation is a function of x only and RHS is a function of t only.So this equation gets true only when,both LHS and RHS is separately equal to a constant ( say \( -k^2\)). $$\frac{1}{X}\;\frac{\partial^2 X}{\partial x^2} = -k^2 $$ And $$\frac{1}{Tv^2} \;\frac{\partial^2 T}{\partial t^2} = -k^2 $$ Rearranging above two equations, $$\frac{\partial^2 X}{\partial x^2} = -k^2X -->eqn(3)$$ And $$\frac{\partial^2 T}{\partial t^2} = -k^2 v^2 T-->eqn(4) $$ Solution of equation (3) & (4) is given by, $$ X=A_1\;e^{ikx}$$ And $$ T=A_2\;e^{i \omega t}$$ Since \( u(x,t) = X(x)T(t) \) , $$ u(x,t)=A\;e^i(kx \pm \omega t + \phi)$$ Taking the real part of solution , $$\boxed{u(x,t)=A\;sin\;(kx \pm \omega t + \phi)}$$ where\( u(x,t) \) is the vertical displacement of particle in medium.
\( A\) is the amplitude of wave
\( k\) is the wave number or wave vector
\( \phi \) is the initial phase
Velocity of transverse waves through a stretched string
Assume a string is stretched vertically upwards as shown in figure below. Let the tension T acts tangentially at each point. On releasing, the string will start to oscillate vertically or stationary waves gets propagated along the string.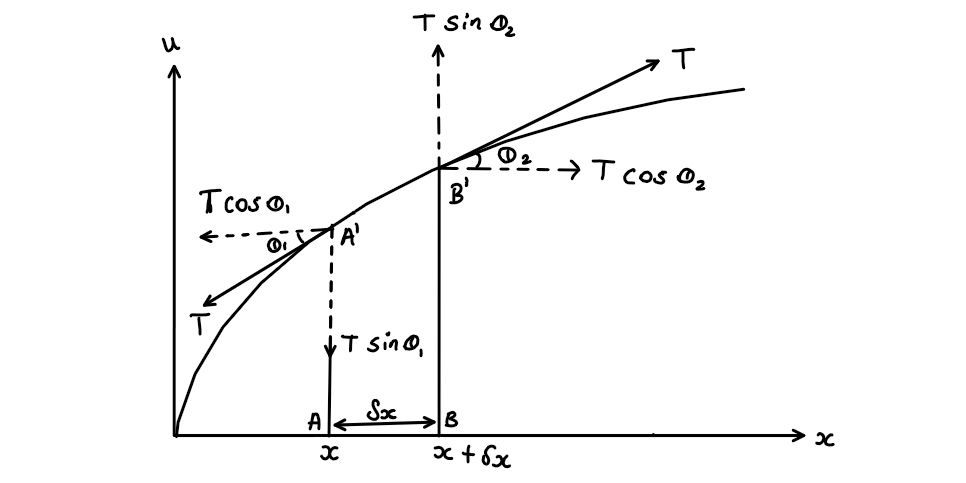
Let \( \theta_1 \) and \( \theta_1 \) be the angle which A' and B' makes with horizontal.
On resolving tension T at points A' and B', total force acting on x direction is given by,
$$F_x = T \;cos\;\theta_2 - T \;cos\;\theta_1 $$ or $$F_x = T (\;cos\;\theta_2 - \;cos\;\theta_1)-->eqn(1) $$ Total force acting vertically ( y direction), $$F_y = T \;sin\;\theta_2 - T \;sin\;\theta_1 $$ or $$F_y = T (\;sin\;\theta_2 - \;sin\;\theta_1) -->eqn(2)$$ Assume that \( \theta_1 \) and \( \theta_2 \) are very small , $$ cos\;\theta_1=cos\;\theta_2= 1 $$ and $$ sin\;\theta_1 = tan\;\theta_1\;\& \; sin\;\theta_2 = tan\;\theta_2$$ Substituting this assumption and expression in equation(1) and (2) ; $$ F_x = 0 $$ Which means resultant force in horizontal direction on string element A'B' is zero and $$ F_y = T (\;tan\;\theta_2 - \;tan\;\theta_1) -->eqn(3)$$ From Newton's second law, force can be represented as, $$F_y=m\;a_y = m\;\frac{\partial^2 y}{\partial t^2}$$ Mass of element A'B' ( of length \( \delta x \)), m can be represented in terms of linear mass density \( \mu \) as, $$m=\mu\;\delta x $$ So, $$F_y=\mu\;\delta x\;\frac{\partial^2 y}{\partial t^2}$$ since \( tan\;\theta \) normally gives slope of a curve at a point, $$tan\;\theta_1=\frac{\partial y}{\partial x} \Big|_{x}$$ $$tan\;\theta_2=\frac{\partial y}{\partial x} \Big|_{x+\delta x}$$ Substituting above expressions and eqn(4) in equation(3); $$ \mu\;\delta x\;\frac{\partial^2 y}{\partial t^2}= T \Big(\;\frac{\partial y}{\partial x} \Big|_{x+\delta x} - \;\frac{\partial y}{\partial x} \Big|_{x}\;\Big)$$ Rearranging, $$ \frac{\mu}{T}\;\frac{\partial^2 y}{\partial t^2}=\frac{\Big(\;\frac{\partial y}{\partial x} \Big|_{x+\delta x} - \;\frac{\partial y}{\partial x} \Big|_{x}\;\Big)}{\delta x}-->eqn(5) $$ From fundamentals of vector calculus, $$ \frac{\Big(\;\frac{\partial y}{\partial x} \Big|_{x+\delta x} - \;\frac{\partial y}{\partial x} \Big|_{x}\;\Big)}{\delta x} = \frac{\partial^2 y}{\partial x^2}$$ Substituting in eqn(5) $$ \frac{\mu}{T}\;\frac{\partial^2 y}{\partial t^2} = \frac{\partial^2 y}{\partial x^2} $$ rearranging, $$ \boxed{\frac{\partial^2 y}{\partial x^2}=\frac{1}{T/\mu}\;\frac{\partial^2 y}{\partial t^2} }$$ Comparing above equation with general wave equation, $$ \boxed{\frac{\partial^2 y}{\partial x^2}=\frac{1}{v^2}\;\frac{\partial^2 y}{\partial t^2} }$$ we get, $$ v^2 = \frac{T}{\mu}$$ That gives velocity of wave through string is given by, $$\boxed{ v =\sqrt{ \frac{T}{\mu}}}$$ where \( T \) is the tension and \( \mu \) is the linear mass density of string.Expression for fundamental frequency
Assume the length of string is \( l \) and it vibrates in n loops. Then length of one loop is given by,
$$ l_{one_loop}=\frac{Total\;length}{no: \;of\;loops}=\frac{l}{n}$$ Since length of one loop is equivalent to half wavelength, $$ \frac{l}{n} = \frac{\lambda}{2}$$ or $$ \lambda = \frac{2l}{n} $$ We know that velocity of wave is related to frquency f and wavelength \( \lambda \) as, $$ v=f \lambda $$ substituting for \( \lambda \) and velocity \( v \), $$ \sqrt{\frac{T}{\mu}} =f \times \frac{2l}{n} $$ which gives frequency of waves through stetched string as, $$ f = \frac{n}{2l}\;\sqrt{\frac{T}{\mu}} $$ When n = 1 , fundamental frequency is given by, $$\boxed{ f_{fundamental} = \frac{1}{2l}\;\sqrt{\frac{T}{\mu}}} $$Laws of vibration
-
Law of length
Fundamental frequency of transverse waves through a stretched string is inversely proportional to length of string.
$$ f_{fundamental} \propto \frac{1}{l}$$ -
Law of tension
Fundamental frequency of transverse waves through a stretched string is directly proportional to square root of tension in the string
$$ f_{fundamental} \propto \sqrt{T}$$ -
Law of mass
Fundamental frequency of transverse waves through a stretched string is inversely proportional square root of linear mass density of string
$$ f_{fundamental} \propto \frac{1}{\sqrt{\mu}}$$
Numerical questions.
- The equation of transverse wave travelling along a stretched string is given by, $$y(x,t) = 30 sin ( 0.5x - 6t + \pi ) $$ where y and x are in cm and t is in second. Find the amplitude, frequency, velocity, wavelength, wave number and initial phase of the wave.