Quantum Mechanics
Quantum mechanics is a branch of physics that describes the behavior of matter and energy at the atomic and subatomic level. It is necessary to understand the properties of these tiny particles that make up everything in the universe.
Matter Waves & De Broglie Wave Hypothesis
In 1924, Louis de Broglie proposed that all matter has wave-like properties, just like light. He called these matter waves. The wavelength of a matter wave is inversely proportional to the momentum of the particle. This is known as the de Broglie wave hypothesis.
De broglie wavelength of a particle with mass m moving with a momentum p is given by, $$\boxed{\;\lambda_{de-broglie}=\frac{h}{p}=\frac{h}{mv}}$$ where h is called planks constant and v is the velocity of particle.Heisenberg's Uncertainty Principle
Position-momentum uncertainty principle
Heisenberg’s uncertainty principle states that it is impossible to measure exact value of both position and the momentum of a moving object. It can also be stated as more precisely the position of a particle is known, the less precisely its momentum can be known, and vice versa.
Mathematically this can be represented as, $$\boxed{ \Delta x \;\Delta p \ge \frac{\hbar}{2} }$$ where \( \Delta x \) and \( \Delta p\) are uncertainities in measurement of position and momentum respectively.Energy-Time uncertainty principle
The energy-time uncertainty principle states that the more precisely the energy of a system is known, the less precisely the duration in which system remains in that energy level can be known, and vice versa.
Mathematically this can be represented as, $$\boxed{ \Delta E \;\Delta t \ge \hbar }$$ where \( \Delta E \) is uncertainty in measurement of energy and \( \Delta t \) is time which particle stays with same energy.Applications of Uncertainty principle
Natural line broadening
Natural line broadening is an example of how the uncertainty principle can affect the properties of a physical system. Specifically, it refers to the phenomenon where the spectral lines of atomic or molecular transitions in a gas or solid are broadened, or spread out.According to Energy-time uncertainty principle, $$\Delta E \;\Delta t \ge \frac{\hbar}{2} $$ or $$ \Delta E = \frac{\hbar}{2 \Delta t} $$ Normally the life time \( \Delta t \) of an atomic energy state \( E\) is \( 10^{-8} \;\) seconds. So according to above equation, minimum uncertainty in energy measurement will be, $$ \Delta E = \frac{\hbar}{2 \times 10^{-8}} =5.27 \times 10^{-27}\;J $$ That means there will be a uncertainty in energy measurement and that will be make the spectral line spread from a precise value. This spreading or broadening of spectral lines ( spectrum of atomic transitions is way to measure energy levels in atom or molecules ) due to this theoretical measurement uncertainty is called natural line broadening.
Non-existence of electrons inside nucleus
If electrons is present in nucleus, the maximum uncertainty in position measurement of this electron inside nucleus will be in order of nuclear diameter (\(10^{-15}\;m\)).According to position-momentum uncertainty principle,
$$\Delta x \;\Delta p \ge \frac{\hbar}{2} $$ Since maximum uncertainty, \( \Delta x = 10^{-15}\;m \), $$\Delta p =\frac{\hbar}{2\;\Delta x} =\frac{\hbar}{2\times10^{-15} }=1.05 \times 10^{-20}\;kg\;m/s.$$ That means momentum should be in order of \(1.05 \times 10^{-20}\;kg\;m/s \).The energy of this electron is calculated with relativistic formula, $$E=pc = 1.05 \times 10^{-20} \times 3 \times 10^8 $$ $$E = 3.15 \times 10^{-12}\;J = 19.6\;MeV$$
Theoretical calculations indicate that for an electron to exist within the nucleus, it would require an energy of around 19.6 MeV. However, experimental observations show that electrons emitted during beta decay have energies of only around 3 MeV, which is significantly lower than the required energy. Additionally, experiments have shown that no electrons or particles within atoms possess energies greater than 4 MeV, further supporting the idea that electrons do not exist within the nucleus.Wavefunction and Physical Significance
In quantum mechanics, the wavefunction is a mathematical function that describes the state of a particle. Wavefunction is normally represented using greek letter \( \Psi\).
The wavefunction itself has no physical meaning. The physical significance is that, we can derive all the known properties of particle from this wavefunction using some mathematical operators.For example the probability density of finding particle ( with wavefunction \(\Psi\)) in a particular location ( say between \( x=a \) and \( x=b \)) is given by $$position\;probability=\int_{a}^{b} \Psi \Psi^* dx$$
Requirements of wavefunction
All mathematical function cannot be a wavefunction, because wavefunction is a complex function that represents a real particle. So wavefunction should have some requirements such as,- The wave function ψ must be continuous and single valued.
- All the partial derivatives of wavefunction such as \( \frac{\partial \Psi }{\partial x } , \;\frac{\partial \Psi }{\partial y },\;\frac{\partial \Psi }{\partial z }\) must also be continuous and single valued.
- Wavefunction must be normalized.
Quantum Mechanical Operators
In quantum mechanics, operators are mathematical objects that act on the state of a quantum system. They are represented by matrices or differential operators, and they can be used to represent physical observables such as position, momentum, energy, and spin.For example, the position operator in one dimension, denoted as \( \hat{x}\).
The wave function \( \psi(x)\) of a particle is an eigenfunction of the position operator, meaning that: $$ \hat{x} \;\psi(x) = x \;\psi(x) $$ where \(\hat{x} \) is position operator acted on wavefunction or eigenfunction \( \psi(x)\) to give position \(x\) as it's eigen value.
Similarly, the momentum operator in one dimension, denoted as \( \hat{p}\), is represented by the differential operator: $$ \hat{p} = -i\hbar \frac{\partial}{\partial x} $$ Where \( \hbar\) is the reduced Planck constant.
The wave function \( \psi(x) \) of a particle is also an eigenfunction of the momentum operator, meaning that: $$ \hat{p} \;\psi(x) = p \;\psi(x) $$ where \(\hat{p} \) is momentum operator acted on wavefunction or eigenfunction \( \psi(x)\) to give momentum \(p\) as it's eigen value.Also the energy operator denoted as \( \hat{E}\), is represented by the differential operator: $$ \hat{E} = i\hbar \frac{\partial}{\partial t} $$
Schrödinger Equation
Time dependent Schrödinger Equation
The Schrödinger equation is a fundamental equation in quantum mechanics that describes how the wavefunction of a particle evolves over time. It is a partial differential equation that relates the energy of a particle to its wavefunction.
where k is the wave number and \( \omega \) is the angular frequency of wave.
From de-broglie wave hypothesis,
$$ \lambda=\frac{h}{p} $$Rearranging above equation,
$$ p=\frac{h}{\lambda} = \frac{h}{ 2 \pi}\times \frac{2 \pi}{\lambda} = \hbar k $$ or , $$\boxed{ k = \frac{p}{\hbar }-->eqn(2)}$$ From Einstein's formula for photon energy, $$ E=h \nu=\frac{h}{2 \pi} \times 2 \pi \nu =\hbar \omega $$ or $$\boxed{ \omega = \frac{E}{\hbar} -->eqn(3)}$$ Substituting these values in eqn(1), we get $$ \Psi(x, t)=A \exp \left[\frac{i}{\hbar}(p x-E t)\right] -->eqn(4) $$ Differentiating eqn(4) with respect to x, we get $$ \frac{\partial \Psi}{\partial x}=\left(\frac{i p}{\hbar}\right) A \exp \left[\frac{i}{\hbar}(p x-E t)\right]=\frac{i p}{\hbar} \Psi $$ Again differentiating w.r.t x, we get $$ \frac{\partial^{2} \Psi}{\partial x^{2}}=\left(\frac{i p}{\hbar}\right)^{2} A \exp \left[\frac{i}{\hbar}(p x-E t)\right]=-\frac{p^{2}}{\hbar^{2}} \Psi $$ That gives \( p^2 \Psi \) as, $$\boxed{ p^2 \Psi = -{\hbar^{2}}\;\frac{\partial^{2} \Psi}{\partial x^{2}}}--eqn(5)$$ Differentiation of eqn(4) with respect to t gives $$ \frac{\partial \Psi}{\partial t}=\left(-\frac{i E}{\hbar}\right) A \exp \left[\frac{i}{\hbar}(p x-E t)\right]=-\frac{i E}{\hbar} \Psi $$ That gives \( E \Psi \) as , $$ \boxed{E \Psi= i \hbar \frac{\partial \Psi}{\partial t}-->eqn(6) }$$ Energy of a particle is given by, $$ E=\frac{p^{2}}{2 m} $$ Multiplying equation with \( \Psi \), $$ E \Psi=\frac{p^{2}\;\Psi}{2 m} $$ Substituting expression for \( E \Psi \) and \( p^2 \Psi \), $$ i \hbar \frac{\partial \Psi}{\partial t}=-\frac{\hbar^{2}}{2 m} \frac{\partial^{2} \Psi}{\partial x^{2}} $$ or $$ \boxed{-\frac{\hbar^{2}}{2 m} \frac{\partial^{2} \Psi}{\partial x^{2}}=i \hbar \frac{\partial \Psi}{\partial t}} -->eqn(6)$$ Equation (6) is the one dimensional time dependent Schrödinger equation for a free particle. In three dimensions, the equation becomes $$ -\frac{\hbar^{2}}{2 m}\left(\frac{\partial^{2} \Psi}{\partial x^{2}}+\frac{\partial^{2} \Psi}{\partial y^{2}}+\frac{\partial^{2} \Psi}{\partial z^{2}}\right)=i \hbar \frac{\partial \Psi}{\partial t}$$ $$-\frac{\hbar^{2}}{2 m}\;\nabla^{2} \Psi=i \hbar \frac{\partial \Psi}{\partial t}$$ where,\( \nabla^{2} \) is called laplacian operator. $$\nabla^{2}=\frac{\partial^{2}}{\partial x^{2}}+\frac{\partial^{2}}{\partial y^{2}}+\frac{\partial^{2}}{\partial z^{2}} $$ If particle is moving under a potential V(r,t), $$ -\frac{\hbar^{2}}{2 m}\;\nabla^{2} \Psi + V\Psi=i \hbar \frac{\partial \Psi}{\partial t} $$ or $$ (-\frac{\hbar^{2}}{2 m}\;\nabla^{2} + V)\;\Psi=i \hbar \frac{\partial \Psi}{\partial t} $$ where \( (-\frac{\hbar^{2}}{2 m}\;\nabla^{2} + V) \) is called hamiltonian operator H, So schrodinger's time dependent equation can be represented as, $$ \boxed{H \Psi = E \Psi}$$Time-independent Schrödinger Equation
Total energy of a particle moving in any potential is given by, $$E = \frac{p^2}{2m} + V $$ rearranging equation, $$ E-V = \frac{p^2}{2m}$$ or, $$\frac{p^2}{2m} = E-V$$ Multiplying with \( \Psi \) on both sides, $$\frac{p^2}{2m}\;\Psi = (E-V)\Psi$$ $$\frac{p^2 \;\Psi}{2m}= (E-V)\Psi$$ Substituting value of \(p^2 \;\Psi \) from eqn(5), $$ -\frac{\hbar^{2}}{2 m} \frac{\partial^{2} \Psi}{\partial x^{2}} = (E-V)\Psi $$ $$ \frac{\hbar^{2}}{2 m} \frac{\partial^{2} \Psi}{\partial x^{2}} + (E-V)\Psi = 0 $$ Multiplying with \( \frac{2m}{\hbar^2} \), $$\boxed{ \frac{\partial^{2} \Psi}{\partial x^{2}} + \frac{2m}{\hbar^2}\;(E-V)\Psi = 0} $$ This is called Schrodinger's time independent equation.Particle in a Square Well Potential
Assume that a particle of mass m is trapped inside a box or infinite square well potential of width L.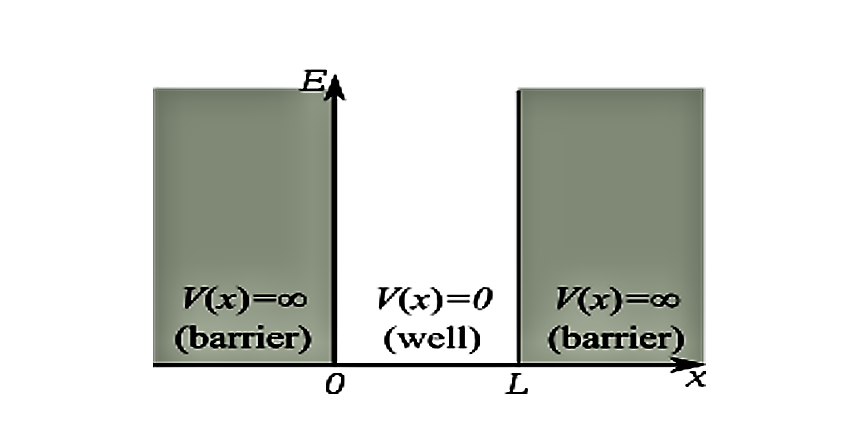
The potential \(V(x)\) is given by \begin{equation} V= \begin{cases} 0 & \text{if}\ 0 \le x \le L \\ & \text{}\ \\ \infty & \text{if} \ x < 0 \;and\; x> L \\ \end{cases} \end{equation}
For deriving the properties of the particle, take Schrödinger's time independent equation, $$ -\frac{\hbar^{2}}{2 m} \frac{d^{2} \psi(x)}{d x^{2}}=(E-V) \psi(x) $$ Consider the region \( 0 \leq x \leq a\) where \( V=0 \). The time independent Schrödinger equation for this region is: $$ \frac{-\hbar^{2}}{2 m} \frac{d^{2} \psi}{d x^{2}}=E \psi $$ or $$\frac{d^{2} \psi}{d x^{2}}=\frac{2 m E}{\hbar^{2}}\; \psi$$ Let , $$ k^{2}=\frac{2 m E}{\hbar^{2}}-->eqn(1) $$ where \(k^2\) is a constant.That makes above equation, $$\frac{d^{2} \psi}{d x^{2}}=-k^{2} \psi $$ The solution of this equation is $$ \psi=A \sin k x+B \cos k x $$ To determine the constants, we have to use the boundary conditions \( \psi=0 \; at \;x=0\) and at \(x=L \).The condition \(\psi=0\; at \;x=0\) leads to \(B=0\).
That gives, $$ \psi=A \sin k x-->eqn(2) $$ The condition \( \psi=0\; at \;x=L\) gives, $$A \sin k L=0$$ The constant \( A\) cannot be zero, since this would make the function zero everywhere. Hence, $$ \sin k L=0 $$ That gives $$kL=n \pi $$ or $$ k=\frac{n \pi}{L} -->eqn(3)$$ Substituting this expression of k in eqn(2), $$ \psi = A \;sin\;\Big(\frac{n \pi}{L}\;x \Big)-->eqn(4)$$To find the value of A :
Apply normalization condition , $$\int_{0}^{L} \psi \;\psi^* \;dx = 1 $$ Substituting \( \psi \) and \( \psi^* \), $$ \int_{0}^{L} A^2 sin^2\;\Big(\frac{n \pi}{L}\;x \Big)\;dx=1 $$ Integrating the function and rearrangement inturn gives the value of A as, $$A=\sqrt{\frac{2}{L}}$$ Substituting value of A in eqn(4), eigen wavefunction of particle is given as, $$\boxed{\; \psi = \sqrt{\frac{2}{L}} \;sin\;\Big(\frac{n \pi}{L}\;x \Big)\;}$$Energy eigen values
From equation (1), $$k^{2}=\frac{2 m E}{\hbar^{2}}$$ and from equation (3), $$k=\frac{n \pi}{L}$$ or $$k^2=\frac{n^2\;\pi^2}{L^2}$$ Comparing the above expressions of \( k^2 \), $$\frac{2 m E}{\hbar^{2}} = \frac{n^2\;\pi^2}{L^2} $$ That gives energy of nth energy state as, $$ E_{n}=\frac{n^{2} \pi^{2} \hbar^{2}}{2 m ^L{2}}$$ These are the possible energy eigenvalues for the particle in the one dimensional box. In terms of plank's constant \( h\), Energy of nth level is given by, $$\boxed{\;\; E_{n}=\frac{n^{2} h^{2}}{8 m L^{2}}\;\;}$$ Eigen function and energy eigen value can be plotted as in figure below.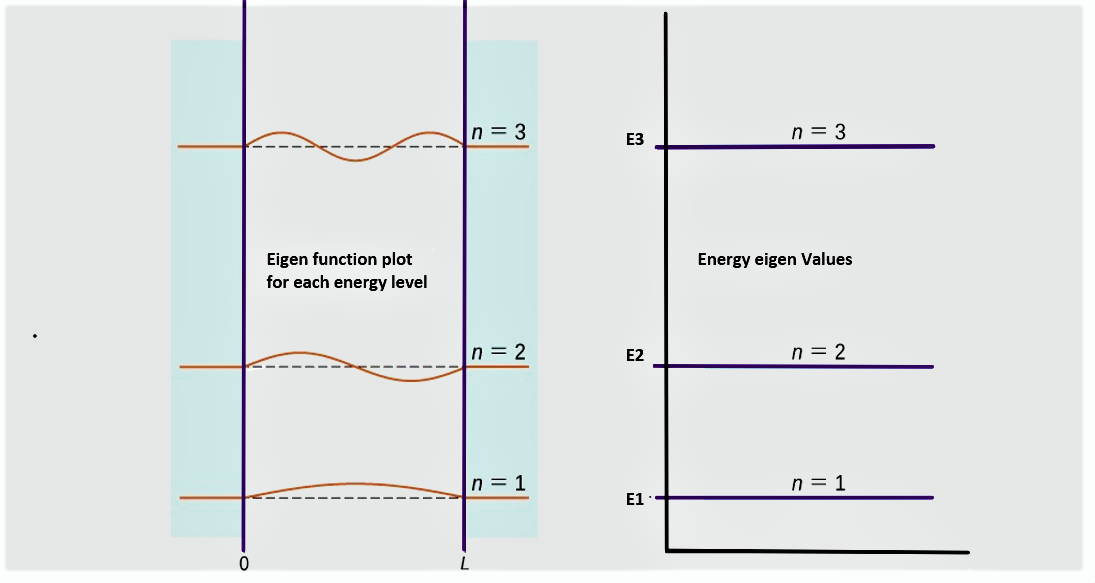
Quantum Mechanical Tunnelling
Quantum mechanical tunneling is a phenomenon where particles, such as electrons, can pass through barriers that they would not be able to pass through classically. This is due to the wave-like nature of particles in quantum mechanics, which allows them to exist in multiple locations simultaneously. As a result, there is a small probability that a particle will be found on the other side of a barrier, even if its energy is not sufficient to pass over the barrier.