Periodic motion
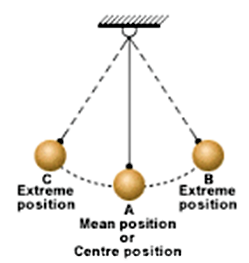
A motion which repeat itself after equal intervals of time is called periodic motion
Examples :
- Motion of planets around sun
- Oscillations of simple pendulum
- Circular motion
Time Period
Time taken by body ( which oscillates) to complete one full cycle or one complete oscillation is called time period of that oscillation.
Examples :
- Earth takes 365 days to complete one complete revolution around sun, So time period of that motion is 365 days.
Oscillatory Motion
Periodic motion in which body moves to and fro about a fixed point is called oscillatory motion.
Some examples of oscillations include:
- A pendulum swinging back and forth
- A mass attached to a spring oscillating up and down
- The oscillation of an electric current in an AC circuit
Frequency
Number of oscillations completed in unit time ( or 1 second ) is called frequency of an oscillator.
Unit of frequency is Hertz ( Hz ) or \(s^{-1}\)
Example :
- If the bob of a simple pendulum completes 3 oscillations in a second, then the frequency of that oscillator is 3 Hz
Simple Harmonic Motion
Simple Harmonic Motion (SHM) is type of oscillation in which restoring force is directly proportional to displacement of body from mean position. The direction of this restoring force is always directed towards the mean position.
Heinrich Hertz
Heinrich Rudolf Hertz was a German physicist born in 1857 and is widely recognized for his contributions to the field of electromagnetism. Hertz conducted experiments that confirmed the existence of electromagnetic waves, which had been predicted by James Clerk Maxwell's theory of electromagnetism. In recognition of his groundbreaking work, the unit of frequency, one cycle per second, was named the "hertz" in his honor.
CloseSimple Pendulum
When a pendulum is displaced from its equilibrium position, it experiences a restoring force due to gravity that acts to return the pendulum to its equilibrium position. This restoring force is proportional to the displacement of the pendulum from its equilibrium position, and acts in the opposite direction to the displacement.
CloseSpring-Mass system
An oscillation of a spring-mass system refers to the back-and-forth motion of a mass attached to a spring that is fixed at one end. When a mass is attached to a spring and is displaced from its equilibrium position, the spring exerts a restoring force that is proportional to the displacement. The mass then oscillates back and forth around its equilibrium position with a frequency determined by the mass and the stiffness of the spring.
CloseSome examples of SHM include
- Swinging of a pendulum
- Oscillation of a mass on a spring
- Vibration of a guitar string
Differential equation representing an SHM is given by :
$$ \frac{d^2 x}{dt^2}+\omega^2 x = 0 $$The equation of motion for SHM is given by:
Where:
- x(t) is the displacement at time t.
- A is the amplitude of oscillation.
- \( \omega\) is the angular frequency of the oscillator.
- \( \phi\) is the initial phase (m)
The angular frequency of SHM is given by:
Since angular frequency is related to frquency as,
$$f=\frac{\omega}{2\pi}$$so,frequency of SHM is given by
$$ f=\frac{1}{2\pi}\sqrt{\frac{k}{m}} $$And time period :
$$T=\frac{1}{f}=2\pi \sqrt{\frac{m}{k}} $$Where:
- k is the force constant (N/m).
- m is the mass of the body (kg).
Free Oscillations
Oscillations in which total energy remains constant ( no energy is lost ) during the motion are called free oscillations. If no external force acts on the oscillator, it continue to oscillate for indefinite ( infinite ) period without change in energy or amplitude.
Damped Harmonic Oscillation
In real situations, energy of an oscillator will lost or gets dissipated to surroundings which will reduce amplitude and eventually leading to the oscillator's stopping. This dissipation of energy due to an external force is called damping. Such oscillators are called damped harmonic oscillators.
Example:
- An oscillating simple pendulum dipped in water
- An electronic circuit with a resistor and capacitor in series is an example of a damped oscillator. The resistor dissipates energy as heat, causing the amplitude of the oscillations in the circuit to decrease over time.
Differential equation of damped harmonic Oscillator
A particle undergoing damped harmonic oscillation will experience (or acted upon by ) two type of forces,
-
Restoring force
Restoring force of harmonic oscillator is given by,
$$F_{restoring}=-kx$$where k is the force constant
-
Damping force
Restoring force of an oscillator is proportional to velocity,
$$F_{damping} \propto -v$$Substituting with a proportionality constant
$$F_{damping}=-bv = -b\;\frac{dx}{dt}$$where b is called damping constant
So total force acting on the particles is,
$$F_{total}=F_{restoring}+F_{damping} $$ $$ F = -b\;\frac{dx}{dt} + -kx = -b\;\frac{dx}{dt} -kx $$From newton's second law, \(F=ma=m\frac{d^2 x}{dt^2}\). Substituting in above equation ;
$$ m\frac{d^2 x}{dt^2}=-b\;\frac{dx}{dt} -kx $$rearranging above equation,
$$ m\frac{d^2 x}{dt^2}+ b\;\frac{dx}{dt} + kx = 0 $$Dividing whole equation with m ;
$$ \frac{d^2 x}{dt^2}+ \frac{b}{m}\;\frac{dx}{dt} + \frac{k}{m}\;x = 0 \; -->eqn(1)$$Let \(\frac{b}{m}=2 \gamma \), where \( \gamma\) is called damping coefficient and \( {\frac{k}{m}}=\omega_o^2 \) where \( \omega_o\) is the angular frequency of oscillator.
On substituting \(2 \gamma \) and \( \omega_o^2\) , differential equation (1) becomes,
$$\boxed{ \frac{d^2 x}{dt^2}+ 2 \gamma \;\frac{dx}{dt} + \omega_o^2 x = 0 }\; -->eqn(2) $$Solution of differential equation
Assume that solution eqn (2) is given by,
$$x=A\;e^{\alpha \;t} $$where A and \(\alpha\) are some arbitrary constants. Differentiating this displacement or \( x \) w.r.t \(t\),
$$\frac{dx}{dt}=\frac{d}{dt}(A\;e^{\alpha \;t})=A\times e^{\alpha \;t} \times \alpha = \alpha A\;e^{\alpha \;t}$$ $$\frac{dx}{dt}=\alpha x $$Taking the differntial of \(\frac{dx}{dt}\) again w.r.t t;
$$\frac{d^2 x}{dt^2}=\frac{d}{dt}(\frac{dx}{dt})=\frac{d}{dt}(\alpha x) $$ $$= \alpha \times \frac{dx}{dt} = \alpha \times \alpha x = \alpha^2 x $$Substituting the expression of \(\frac{dx}{dt}\) & \(\frac{d^x x}{dt^2}\) in equation (2) ;
$$\alpha^2 x+ 2 \gamma \alpha x + \omega_o^2 x = 0 $$Dividing by x,
$$\alpha^2 + 2 \gamma \alpha + \omega_o^2 = 0 $$This is a quadratic equation with solution,
$$\alpha = \frac{-2 \gamma \pm \sqrt{4 \gamma^2 - 4 \omega_o^2}}{2}$$ $$=- \gamma \pm \sqrt{ \gamma^2 - \omega_o^2} $$Since \( x=A\;e^{\alpha \;t} \) & substituting value of \(\alpha\) ;
$$x=A\;e^{(- \gamma \pm \sqrt{ \gamma^2 -\omega_o^2})\;t} $$So the two solutions of equation are :
$$x_1=A_1\;e^{(- \gamma + \sqrt{ \gamma^2 -\omega_o^2})\;t} $$ $$x_2=A_2\;e^{(- \gamma - \sqrt{ \gamma^2 -\omega_o^2})\;t} $$Therefore the general solution is
$$x=x_1 + x_2 $$ $$ x = A_1\;e^{(- \gamma + \sqrt{ \gamma^2 -\omega_o^2})t} + A_2\;e^{(- \gamma - \sqrt{ \gamma^2 -\omega_o^2})t} $$where \(A_1\) and \(A_2\) are constants which depends on the initial values of position and velocity.
Cases of damping
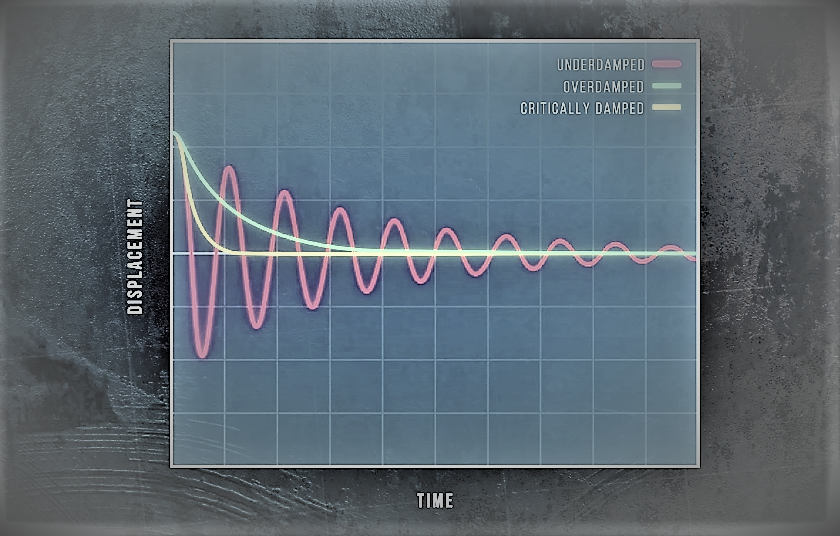
Overdamping ( \(\gamma > \omega \) )
In this case damping is very high. Since \(\gamma > \omega \) , solution in this case is ( refer eqn(2)),
$$ x = A_1\;e^{- \gamma + \sqrt{ \gamma^2 -\omega_o^2}} + A_2\;e^{- \gamma - \sqrt{ \gamma^2 -\omega_o^2}} $$Since \(\gamma > \omega \), the term \(\sqrt{ \gamma^2 -\omega_o^2}\) will be a real quantity and will be less that \( \gamma \). That means terms (\(- \gamma + \sqrt{ \gamma^2 -\omega_o^2}\)) and (\(- \gamma + \sqrt{ \gamma^2 -\omega_o^2}\)) are both negative. So the displacement \(x\) decays exponentially to zero without any oscillation.
Critical damping ( \(\gamma = \omega \) )
Since \(\gamma = \omega \) , the term \(\sqrt{ \gamma^2 -\omega_o^2}\) will become zero. So the solution in this case is,
$$ x = A_1\;e^{- \gamma t} + A_2\;e^{- \gamma t} $$ $$x = (A_1 + A_2) \;e^{- \gamma t}$$let \(C = A_1 + A_2\),
$$ x = C\;e^{- \gamma t} $$So the displacement decreases instantanously when time 't' passes. So the displacement \(x\) decays exponentially to zero without any oscillation.
Under damping ( \(\gamma < \omega \) )
In this case damping is very low. Since \(\gamma < \omega \) , the term \(\sqrt{ \gamma^2 -\omega_o^2}\) will be imaginary. Using euler's theorem and some mathematical re arrangements, the expression of displacement can be written as,
$$\boxed{x=A\;e^{-\gamma t} \;sin(\omega t + \phi)}$$where \( \omega = \sqrt{\omega_o^2 - \gamma^2} \) and
\(A\;e^{- \gamma t}\) is the amplitude of oscillation which decreases over time. That means underdamped oscillator is oscillatory, but decays energy eventually when time passes.
Quality factor
The term quality factor defines the quality or efficiency of oscillator. For example, a high Q - factor represents a lower rate of energy loss.
Eg : A pendulum oscillating in air will have a high Q factor comparing to a pendulum oscillating inside water or any liquid.
Quality factor can be mathematically represented as,
$$Q = 2 \pi \times \frac{Energy\;stored\;in\;an \;oscillator}{Energy\;lost\;per\;cycle}$$or,
$$Q = 2 \pi \frac{Energy\;stored\;in\;an \;oscillator}{Energy\;lost\;per\;second \times Period}$$If \(E\) is the energy of oscillator,
$$Q= 2 \pi \times \frac{E}{-\frac{dE}{dt} \times T} \;-->eqn[1]$$Since the energy loss in a damped oscillator is represented as
$$E=E_o e^{-2 \gamma t} $$differentiating w.r.t \(t\) ,
$$\frac{dE}{dt}= - 2 \gamma E $$Substituting in equation (1) ,
$$Q= 2 \pi \times \frac{E}{-\frac{dE}{dt} \times T} = 2 \pi \times \frac{E}{2 \gamma E \times T} $$writing timeperiod T in terms of angular frequency \( \omega \),
$$Q = 2 \pi \times \frac{E}{2 \gamma E \times \frac{2 \pi}{\omega}} $$That gives expression for quality factor as,
$$\boxed{Q \;-\; factor =\frac{\omega}{2 \gamma} }$$Where \( \gamma \) is damping coefficient.
Relaxation time
The time which an oscillator takes to reduce it's energy to \(\frac{1}{e}\) th of initial (un-damped) energy is called relaxation time
$$Relaxation\;time\;\tau=\frac{1}{2 \gamma} $$so quality factor can be represented in terms of relaxaation time as,
$$ Q =\frac{\omega}{2 \gamma} = \omega \;\tau $$Forced Harmonic Oscillation
If an external force is applied to a damped harmonic oscillator, such oscillators are called forced harmonic oscillators.
Example:
- A swing repeatedly pushed by someone
- LCR circuit
Differential equation of forced harmonic Oscillator
A particle undergoing forced harmonic oscillation will experience (or acted upon by ) three types of forces,
-
Restoring force
Restoring force of harmonic oscillator is given by,
$$F_{restoring}=-kx$$where k is the force constant
-
Damping force
Damping force on oscillator is given as,
$$F_{damping}= -b\;\frac{dx}{dt}$$where b is called damping constant
-
External periodic force
When a force is periodically applied to a damped oscillator, it can be represnted as
$$F_{external}=F_o\;sin(\omega_f \;t)$$where \(F_o\) is the external force amplitude and \(\omega_f\) is the frequency of external force or called as external driving frequency.
So total force acting on the particles is,
$$F_{total}=F_{restoring}+F_{damping}+F_{external} $$ $$ F = -kx -b\;\frac{dx}{dt} +F_o\;sin(\omega_f \;t) $$From newton's second law, \(F=ma=m\frac{d^2 x}{dt^2}\). Substituting in above equation ;
$$ m\frac{d^2 x}{dt^2}=-kx -b\;\frac{dx}{dt}+F_o\;sin(\omega_f \;t)$$rearranging above equation,
$$ m\frac{d^2 x}{dt^2}+ b\;\frac{dx}{dt} + kx = F_o\;sin(\omega_f \;t) $$Dividing whole equation with m ;
$$ \frac{d^2 x}{dt^2}+ \frac{b}{m}\;\frac{dx}{dt} + \frac{k}{m}\;x = \frac{F_o}{m}\;sin(\omega_f \;t) $$Let \(\frac{b}{m}=2 \gamma \), where \( \gamma\) is called damping coefficient, \( {\frac{k}{m}}=\omega_o^2 \) where \( \omega_o\) is the angular frequency of oscillator and let \(\frac{F_o}{m}= f_o\) where \(f_o\) just another constant .
On substituting above values, differential equation (1) becomes,
$$\boxed{ \frac{d^2 x}{dt^2}+ 2 \gamma \;\frac{dx}{dt} + \omega_o^2 x =f_o\;sin(\omega_f \;t) }$$Solution of differential equation
Initially body will not oscillate neither with it's natural frequency (\(\omega_o\)) nor with external driving frequency (\(\omega_f\)). After some time oscillator returns to a steady state, where it will oscillate with external driving frequency \(\omega_f\). So we can assume that solution of eqn (2) as,
$$x=A\;sin(\omega_f \;t -\theta) $$differentiating x w.r.t t ;
$$\frac{dx}{dt}=A\omega_f\;cos(\omega_f \;t -\theta) $$Taking the differntial of \(\frac{dx}{dt}\) again w.r.t t;
$$\frac{d^2 x}{dt^2}=-A \omega_f^2 sin(\omega_f \;t -\theta) $$Substituting the expression of \(\frac{dx}{dt}\) & \(\frac{d^x x}{dt^2}\) in equation (2) ;
$$ -A \omega_f^2 sin(\omega_f \;t -\theta) + 2 \gamma \; (A\omega_f\;cos(\omega_f \;t -\theta))$$ $$\;+ \omega_o^2 (A\;sin(\omega_f \;t -\theta)) = f_o\;sin(\omega_f \;t) $$We can write,\(f_o\;sin(\omega_f \;t) = f_o\;sin(\omega_f \;t-\theta + \theta)\). So,
$$-A \omega_f^2 sin(\omega_f \;t -\theta) + 2 \gamma \; (A\omega_f\;cos(\omega_f \;t -\theta)) $$ $$\;+ \omega_o^2 (A\;sin(\omega_f \;t -\theta))=f_o\;sin(\omega_f \;t-\theta + \theta) $$Expanding term in RHS,
$$-A \omega_f^2 sin(\omega_f \;t -\theta) + 2 \gamma \; (A\omega_f\;cos(\omega_f \;t -\theta)) $$ $$\;+ \omega_o^2 (A\;sin(\omega_f \;t -\theta)) $$ $$= f_o\;[sin(\omega_f \;t -\theta)\;cos\;\theta +sin\;\theta \;cos(\omega_f \;t -\theta)]$$Taking the coefficients of \(sin(\omega_f \;t -\theta)\) and \(cos(\omega_f \;t -\theta)\) from above equation,
$$ sin(\omega_f \;t -\theta)\;[\;-A\omega_f^2 -f_o \;cos\;\theta + \omega^2 A \;] + $$ $$cos(\omega_f \;t -\theta)\;[2\gamma A\omega_f -f_o \;sin\;\theta\;] = 0 $$For equation (3) to be satisfied, coefficients of \(sin(\omega_f \;t -\theta)\) and \(cos(\omega_f \;t -\theta)\) should be separately equal to zero.
$$-A\omega_f^2 -f_o \;cos\;\theta + \omega^2 A = 0 $$ $$ $$ $$2\gamma A\omega_f -f_o \;sin\;\theta = 0 $$or
$$-A\omega_f^2 + \omega^2 A = f_o \;cos\;\theta -->eqn(4)$$ $$ $$ $$2\gamma A\omega_f = f_o \;sin\;\theta\;-->eqn(5) $$squaring and adding equations(4) and (5) ;
$$(-A\omega_f^2 + \omega^2 A)^2 + (2\gamma A\omega_f)^2 =$$ $$=(f_o \;cos\;\theta)^2 + (f_o \;sin\;\theta)^2$$ $$= f_o^2 cos^2 \theta + f_o^2 sin^2 \theta = f_o^2 \;(cos^2 \theta+sin^2 \theta)$$which gives,
$$(-A\omega_f^2 + \omega^2 A)^2 + (2\gamma A\omega_f)^2 = f_o^2 $$or
$$ A^2[\;(\omega^2 - \omega_f^2)^2 + 4 \gamma^2 \omega_f^2\;]=f_o^2 $$That gives,
$$A^2 = \frac{f_o^2}{(\omega^2 - \omega_f^2)^2 + 4 \gamma^2 \omega_f^2} $$so amplitude of oscillator is obtained as,
$$\boxed{A = \frac{f_o}{\sqrt{(\omega^2 - \omega_f^2)^2 + 4 \gamma^2 \omega_f^2}}} $$Hence the solution of differential equantion is,
$$x = \frac{f_o\;sin(\omega_f t - \theta)}{\sqrt{(\omega^2 - \omega_f^2)^2 + 4 \gamma^2 \omega_f^2}} $$Cases of forced oscillator
Case 1: High driving frequency
When the angular frequency of the driving force, \( \omega_f\), is greater than the natural angular frequency of the oscillator, \( \omega\), the amplitude of oscillation is small.
neglecting the \( \omega^2 \) term in amplitude expression assuming low damping ( \( \gamma \) is very small ) ,
$$ A =\frac{f_o}{\omega_f^2}$$Case 2: Low driving frequency
When the angular frequency of the driving force, \( \omega_f\), is less than the natural angular frequency of the oscillator, \( \omega\), the amplitude of oscillation is also small.
neglecting the \( \omega_f^2 \) term in amplitude expression,
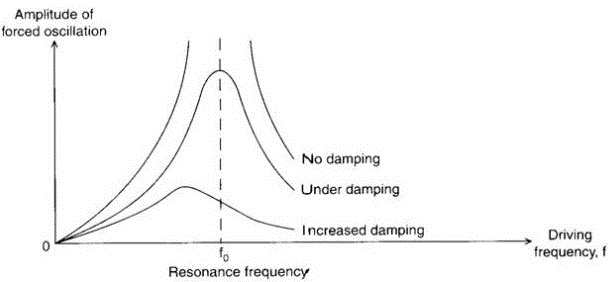
$$ A =\frac{f_o}{\omega^2}$$Case 3: Resonance
When the angular frequency of the driving force, \( \omega_f\), is equal to the natural angular frequency of the oscillator, \( \omega\), the amplitude of oscillation is maximum. This is known as resonance.
That gives expression of maximum amplitude as,
$$ A = \frac{f_o}{4 \gamma \;\omega_f} $$Sharpness of Resonance
In forced harmonic oscillation, the amplitude of oscillation is maximum when the angular frequency of the driving force, \( \omega_f\), is equal to the natural angular frequency of the oscillator, \( \omega\). This is known as resonance.
Sharpness of resonance can also be defined in terms of how the amplitude of oscillation changes with the angular frequency of the driving force.
However, the sharpness of resonance can vary depending on the damping coefficient, \( \gamma\). The sharpness of resonance is determined by the quality factor, Q, which is defined as:
The quality factor, Q, is a measure of the sharpness of resonance. A high Q value indicates a sharp resonance, while a low Q value indicates a broad resonance.
Bandwidth
Bandwidth is the range of angular frequencies over which the amplitude of oscillation is at least half of its maximum value. In other words, it is the range of frequencies between half power points (frequencies at which the power of oscillation is half the peak power).
LCR Circuit
An LCR circuit is a type of electrical circuit that contains a inductor (L), a capacitor (C), and a resistor (R). These components are connected in series, meaning that the current flows through all of them in a single path.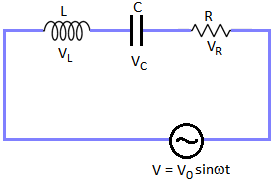
Comparison between Mechanical and Electrical oscillator
| Parameter | Mechanical Oscillators (FHM) | Electrical Oscillators (LCR) |
|---|---|---|
| System | Involves physical displacement | Involves electrical current or voltage |
| Oscillating element | A physical object such as a spring-mass system, a pendulum etc | An electrical component such as an inductor, capacitor or resistor |
| Frequency determining element | The restoring force, such as a spring constant or gravitational force | An LC or RC circuit |
| Damping element | Friction, air resistance, etc. | Resistor |
| Quality factor | Depends on damping coefficient, which is a measure of energy loss | Depends on the ratio of reactance to resistance in the oscillator circuit |
| Frequency range | Low to medium, typically in the range of a few hertz to a few kilohertz | High, typically in the range of kilohertz to gigahertz |
| Applications | Timing devices, musical instruments, mechanical filters, etc. | Radio and television transmitters and receivers, signal generators, etc. |
Related problems
Topic : Quality factor
Formulas : $$E(t) = E_o \ e^{-2\gamma t}$$ where E(t) is the energy of oscillator at time t, \(E_o\) is the initial energy and \(\gamma\) is the damping coefficient. $$A(t) = A_o \ e^{-\gamma t} $$ where A(t) is amplitude of oscillator at time t and \( A_o\) is the initial amplitude. $$Q-factor = \frac{\omega}{2 \gamma}$$ where \( \omega\) is angular frequency of oscillator. $$Q-factor = \frac{A_{max}}{A_{min}} $$ where \(A_{max}\) and \(A_{min}\) are maximum and minimum amplitudes of oscillator respectively.
-
The frequency of a tuning fork is 100 Hz and its Q factor is \(5 \times 10^3\). Find the relaxation time. Also calculate the time after which its energy becomes 1/10 th of its initial un-damped value.
-
A damped harmonic oscillator has a Q factor of \(2 \times 10^3\) and an angular frequency of \(3 \times 10^3\) rad/s. Find the damping coefficient and the time after which the energy of the oscillator becomes 1/e of its initial value.
-
A damped harmonic oscillator has a Q-value of 0.5 and a frequency of 250 Hz. Determine the damping coefficient and the time required for the energy of the oscillator to decrease to half of its initial value.
A damped harmonic oscillator has a Q-value of 0.2 and a frequency of 150 Hz. Find the damping coefficient and the time required for the energy of the oscillator to decrease to 1/3 of its initial value.
-
A damped harmonic oscillator has an angular frequency of 2 rad/s and the time taken for the energy to decrease to 1/2 of its initial value is 3 seconds. Find the quality factor (Q) of the oscillator.
Topic : Quality factor
Formulas : $$E(t) = E_o \ e^{-2\gamma t}$$ where E(t) is the energy of oscillator at time t, \(E_o\) is the initial energy and \(\gamma\) is the damping coefficient. $$A(t) = A_o \ e^{-\gamma t} $$ where A(t) is amplitude of oscillator at time t and \( A_o\) is the initial amplitude. $$Q-factor = \frac{\omega}{2 \gamma}$$ where \( \omega\) is angular frequency of oscillator. $$Q-factor = \frac{A_{max}}{A_{min}} $$ where \(A_{max}\) and \(A_{min}\) are maximum and minimum amplitudes of oscillator respectively.
-
The frequency of a tuning fork is 100 Hz and its Q factor is \(5 \times 10^3\). Find the relaxation time. Also calculate the time after which its energy becomes 1/10 th of its initial un-damped value.
Video gallery
A better description of resonance
Resonance and the Sounds of Music
Resonance Explained !
Amazing Resonance Experiment!