Diffraction
Diffraction is the phenomenon of light bending around obstacles or spreading out when passing through small openings. It is caused by the wave nature of light, which allows it to bend and spread out as it passes through small openings or around obstacles. This results in a diffraction pattern that can be observed on a screen or detector placed behind the diffracting object.
Classification of Diffraction
Diffraction can be classified into two types: Fraunhofer diffraction and Fresnel diffraction.
Fraunhofer Diffraction
Fraunhofer diffraction occurs when the diffracting object is far away from the observer or detector. An example of this is the diffraction of light by a single slit. The diffraction pattern observed on a screen behind the slit is a set of bright and dark fringes, with the bright fringes corresponding to constructive interference and the dark fringes corresponding to destructive interference.
Fresnel Diffraction
Fresnel diffraction occurs when the diffracting object is close to the observer or detector. An example of this is the diffraction of light by a circular aperture, such as the diffraction of light by a circular lens. The diffraction pattern observed on a screen behind the aperture is a set of concentric bright and dark rings, with the bright rings corresponding to constructive interference and the dark rings corresponding to destructive interference.
The table below classifies Fresnel and Fraunhofer diffraction in detail.
| Property | Fresnel Diffraction | Fraunhofer Diffraction |
|---|---|---|
| Distance from source to diffractor | Short (near field) | Long (far field) |
| Distance from diffractor to observer | Long (far field) | Short (near field) |
| Shape of wavefront | Spherical | Plane |
| Diffraction pattern | Circular | Linear |
| Applications |
|
|
Comparison between Interference and Diffraction
| Characteristic | Interference | Diffraction |
|---|---|---|
| Definition | Occurs when two or more light waves overlap and interact with each other | Occurs when light waves encounter an obstacle or opening that is roughly the same size as its wavelength |
| Amplitude of resulting wave | Sum of amplitudes of individual waves | Convolution of amplitude of individual waves |
| Formation of patterns | Bright and dark bands with uniform intensity | Bright and dark bands with varying intensity |
| Width of bands | Uniform | Varying from centre to either sides |
| Dependency on size of obstacle or opening | Dependent on coherence of interferring waves | Directly proportional |
| Observable with | Interference pattern | Diffraction pattern |
| Examples | Young's double-slit experiment, Newton's rings | Single-slit diffraction, diffraction gratings |
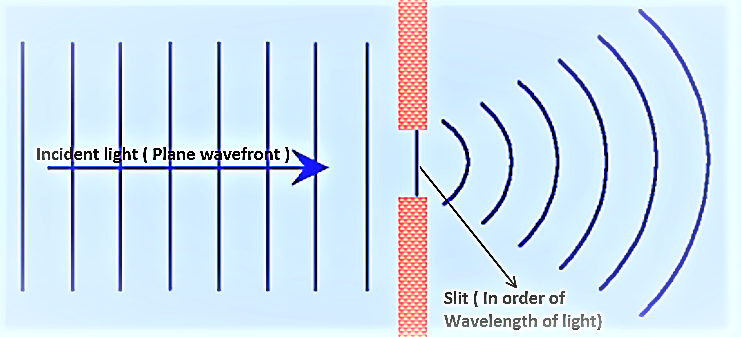
Diffraction Grating
A diffraction grating is a surface with a large number of parallel, closely spaced, and equally spaced
lines or
grooves. In other words grating is an arrangement of tiny slits in glass plate.

Those light waves diffracts in normal direction converges in the central part of screen can be called as central maximum. This point has peak intensity in the diffraction pattern.
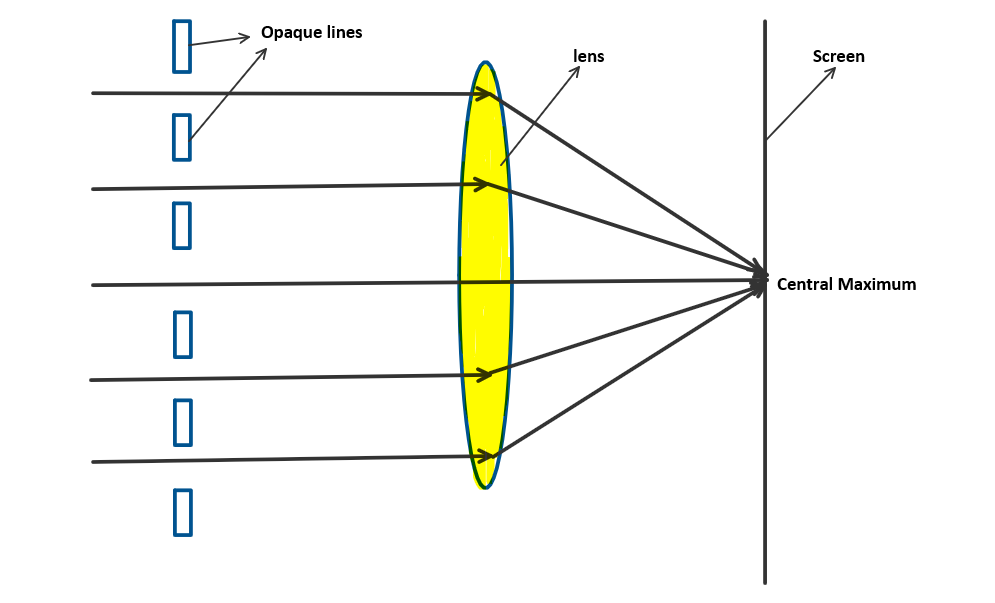
Derivation of grating equation
When incidenting with a monochromatic light, diffraction happens at all points in a grating. That means light gets diffracted ( or say spread ) in all direction at each transparent slit. Take the width of opaque line as b and that of transparent portion as a.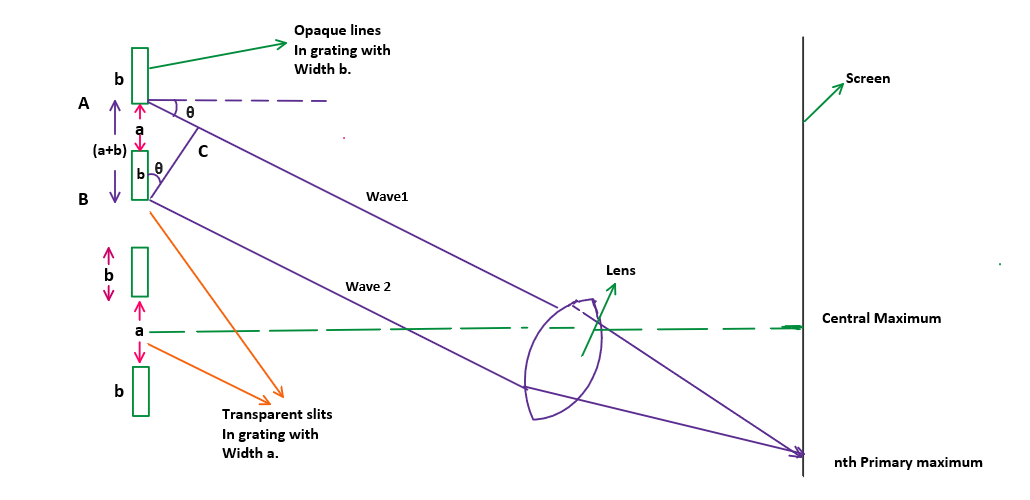
Refer the figure above & take light waves that diffracts in direction \( \theta \) ( making an angle \(\theta\) with horizontal ) from adjacent slits. If these two waves ( wave 1 and wave 2 ) adds each other and converges to form a maximum, the path difference between them should me multiple of wavelength \( \lambda \).
So Condition for forming nth order primary maximum at this point is, $$path\;difference = n\lambda $$ From the figure, path difference between wave1 and wave2 is , $$path\;difference=AC $$ From △ABC, $$sin\;\theta=\frac{AC}{AB} $$ or $$AC=AB\;sin\;\theta $$ Since AB is the total width of opaque line (b) and transparent slit (a), $$ AC = (a+b)\;sin\;\theta $$ That gives condition for forming nth order primary maximum as, $$ (a+b)\;sin\;\theta = n\lambda $$ or $$\boxed{ sin\;\theta = \frac{1}{a+b}\;n\lambda} $$ where \( (a+b)\) is called grating element.Since \(\frac{1}{a+b}= N \) where N is number of lines per unit length in grating, Grating equation can be written as,
$$ \boxed{sin\;\theta=Nn \lambda} $$Where
\( \theta \) is the angle of diffraction
n is the order of spectrum
N is the number of lines per unit length
\( \lambda \) is the wavelength of light used.
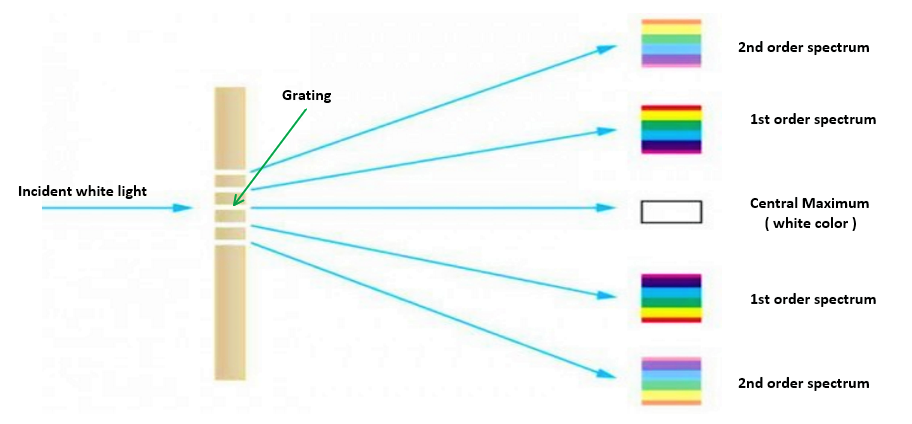
White light on grating
White light contains all the wavelengths in visible spectrum. So when incidenting white light on grating, all these wavelengths will obey the grating equation,
$$ sin\;\theta=Nn \lambda $$ That means each wavelength (\( \lambda \) ) will have unique angle of diffraction \( \theta \) based on their wavelength. Or each color or wavelength in white light will have a unique position in maxima of diffraction pattern.So each primary maximum will be a collection of colors based on their wavelength or we can say a spectrum is formed rather than a single bright spot of maximum at each point.
Rayleigh criterion
The two spectral lines (wavelengths or colors) will be resolved ( seen as separate ) only if atleast primary maximum of any order of one line falls on first order secondary minimum of other one.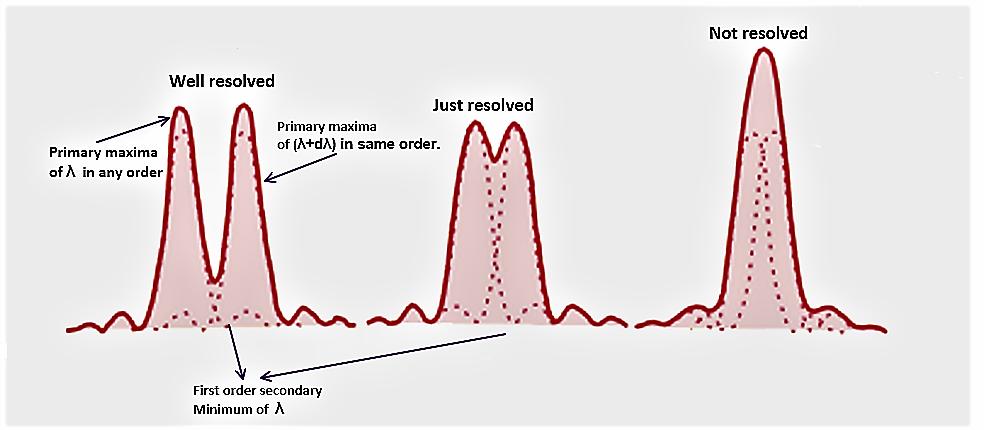
Resolving power of grating
The resolving power of a grating refers to its ability to separate or resolve closely spaced lines or wavelengths in a spectrum. The resolving power of a grating is determined by the number of lines per millimeter (or per inch) on the grating and the angle of incidence of light on the grating.
It is defined as the ratio of the wavelength of one of the spectral line to the difference in the wavelengths between them such that the two lines appear to be just resolved.
Resolving power of grating is given by relation, $$\boxed{ \frac{\lambda}{d \lambda} = N n }$$ where n is the order of spectrum and N is the number of lines per unit length of grating.Dispersive power
The dispersive power of a grating refers to its ability to spread out different wavelengths of light into a spectrum. A grating's dispersive power is determined by the spacing between the lines on the grating and the angle of incidence of light on the grating.
Mathematically dispersive power can be defined change in angle of diffraction ( \( \theta \)) with respect to wavelength \( \lambda \). Dispersive power of grating is given by equation, $$\boxed{\frac{d\theta}{d \lambda}=\frac{N n}{cos\;\theta} }$$ where n is the order of spectrum, N is the number of lines per unit length of grating and \( \theta \) is the angle of diffraction.