Magnetism

Magnetic Field

The magnetic field is a vector field or area in which a charged particle experience a magnetic force. It is created by the motion of electric charges, and it is measured in units of teslas (T) or gauss (G).

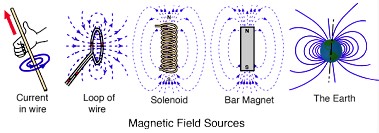
Magnetic flux

Magnetic flux is a measure of the amount of magnetic field passing through a given surface or it is the total number of magnetic field lines passing through an area. It is defined as the product of the magnetic field strength (measured in teslas) and the area of the surface it is passing through (measured in square meters). The unit of magnetic flux is the weber (Wb).

Mathematically, the magnetic flux through a surface can be represented as an integral of the dot product of the magnetic field vector and the area vector over the surface:

$$\Phi = {\mathbf{B} \cdot \mathbf{A}}$$ Where $\Phi$ represents the magnetic flux, $\mathbf{B}$ is the magnetic field vector and $d\mathbf{A}$ is the area of the surface.

Magnetic flux density

Magnetic flux density, also known as the magnetic field strength, is a measure of the amount of magnetic field ( number of magnetic field lines ) per unit area. It is represented by the vector field B and is measured in teslas (T).

The magnetic flux density is related to the magnetic flux, which is a measure of the total magnetic field passing through a given surface. The magnetic flux density is the amount of magnetic flux per unit area.

Mathematically, the magnetic flux density is given by: $$\mathbf{B} = \frac{\Phi}{A}$$ Where $\mathbf{B}$ is the magnetic flux density, $\Phi$ is the magnetic flux, and $A$ is the area of the surface through which the flux is passing.

Gauss's Law

Gauss's law states that the net flux of the magnetic field through a closed surface is equal to zero.

This means that the total number of magnetic field lines entering a closed surface is equal to the number of field lines leaving the surface.

$$\nabla \cdot \mathbf{B} = 0$$ where $ \mathbf{B} $ is the magnetic field and the divergence is taken over a closed surface.

Ampere's Circuital Law

Ampere's circuital law states that the line integral of the magnetic field around a closed loop is equal to the current passing through the loop. This relationship between the magnetic field and current is important in understanding the behavior of electric circuits.

$$\oint_{C} \mathbf{B} \cdot d\mathbf{l} = \mu_0 I$$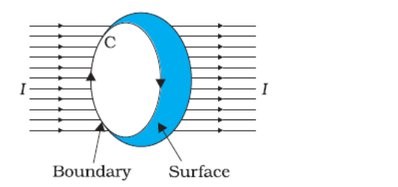

I is total current passing through surface enclosed by boundary C .

where $ \mathbf{B} $ is the magnetic field, $ d\mathbf{l} $ is a differential vector element of a closed path C, $ \mu_0 $ is the permeability of free space, and $ I $ is the current passing through the path.

Faraday's Law

Faraday's law of induction states that a changing magnetic field induces an electromotive force (EMF) in a conductor.

$$emf,\;e = -\frac{d\Phi_B}{dt}$$ where e is the emf arose in the circuit and $\Phi_B $ is the magnetic flux through the closed path.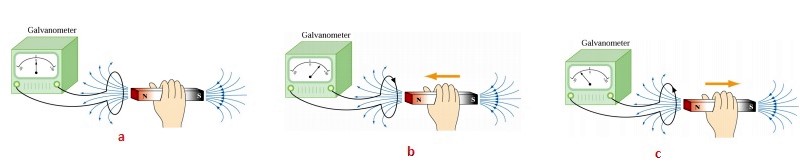

The voltage across galvanometer changes due to emf induced in circuit as a result of change in flux caused by relative movement of magnet.

Magnetic moment

Magnetic moment refers to the strength and direction of a materials magnetic field. It is a measure of the amount of magnetic force that a magnet can exert on other magnets or magnetic materials in its vicinity.

Magnetic moment is typically measured in units of ampere meters squared (A⋅m²) or joules per tesla (J/T).

Magnetization

Magnetization refers to the process by which a material becomes magnetized, that is, it acquires a magnetic moment and the ability to attract or repel other magnetic materials.

When a magnetic field is applied to a material, it can cause the magnetic moments of individual atoms or molecules to align in the direction of the field, increasing the material's overall magnetic moment and creating a net magnetic field. This process is known as induced magnetization.

Left : Alignment of magnetic moments inside specimen before magnetization.
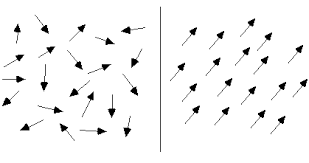
Right : Alignment of magnetic moments inside specimen after magnetization.

Intensity of magnetisation

It is the measure of strength of a magnetic field within a magnetic material after magnetization. It is also defined as magnetic moment per unit volume of material.

$$M=\frac{Magnetic\;moment}{volume}$$ Since moment is related to pole strength m and total length $2l$ as, $$Moment = m \times 2l $$ Intensity of magnetization is defined as, $$M=\frac{m \times 2l}{V}$$ Unit is Ampere per metre.

Magnetic Susceptibilty

Magnetic susceptibility is a measure of how easily a material can be magnetized when an external magnetic field is applied.

It is also defined as the ratio of the magnetization of the material to the applied magnetic field

$$\chi = \frac{\mathbf{M}}{\mathbf{H}}$$

Magnetic Permeability

Magnetic permeability is a measure of a material's ability to conduct magnetic fields or property of a material to allow magnetic field lines pass through it.

It is also defined as the ratio of the magnetic flux density (B) inside material to the magnetic field strength (H) in a material.

$$\mu = \frac{\mathbf{B}}{\mathbf{H}}$$

Relative permeability

Relative permeability is a measure of how easily a material can be magnetized, compared to air or vacuum.

It is defined as the ratio of the magnetic permeability of the material to the permeability of free space.

$$\mu_r=\frac{\mu}{\mu_o}$$ Where $\mu$ is the permeabilty of material and $\mu_o$ is the permeabilty of air or vaccum/free space.

Relation between relative permeability and suscesptibility

The total magnetic flux density inside a material is the sum of the flux density due to the external magnetic field and the flux density due to the intrinsic magnetization of the material, which is a measure of the material's magnetic response to the external field. That means, $$\mathbf{B} = \mu_0 \mathbf{H} + \mu_o \mathbf{M}$$ $$\mathbf{B} = \mu_0(\mathbf{H} + \mathbf{M})$$ where $ \mu_0 $ is the permeability of free space, $ \mathbf{H} $ is the magnetic field strength, and $ \mathbf{M} $ is the magnetization.

From the definition of susceptibilty, magnetization of a material is given by $$\mathbf{M} = \chi \mathbf{H}$$ where $ \chi $ is the susceptibility of the material.

By substituting this expression of M into the first equation, we get $$\mathbf{B} = \mu_0(\mathbf{H} + \chi \mathbf{H})$$ which simplifies to $$\mathbf{B} = \mu_0 \mathbf{H}(1 + \chi) $$ or $$\frac{\mathbf{B}}{\mathbf{H}} = \mu_0 (1 + \chi) $$ We know that $$\mu = \frac{\mathbf{B}}{\mathbf{H}}$$ is the relative permeability of a material. That gives, $$\mu = \mu_0(1 + \chi)$$ Then we can simplify the above equation to get $$\mu_r = 1+\chi$$. Therefore the relationship between relative permeability $ \mu_r $ and susceptibility $ \chi $ is: $$\boxed{\mu_r = 1+\chi}$$

Classification of magnetic materials

Electrons have an intrinsic angular momentum, or spin, which creates a magnetic moment.In most atoms, electrons are paired, meaning that two electrons with opposite spins occupy the same orbital. The magnetic moments of these paired electrons cancel each other out, resulting in no net magnetic moment for the atom.

However, in atoms, ions, or molecules with unpaired electrons, the magnetic moments of the unpaired electrons do not cancel out, resulting in a net magnetic moment for the atom or molecule.

Diamagnetism

Diamagnetism is a property exhibited by some materials that causes them to be weakly repelled by a magnetic field. Unlike paramagnetic materials, which are attracted to a magnetic field, diamagnetic materials are repelled by a magnetic field.

This is due to the presence of paired electrons in the material, which generate a magnetic field that opposes the applied magnetic field. In other words, paired electrons generate a small magnetic moment that opposes an external magnetic field.

Diamagnetic materials have a negative magnetic susceptibility, indicating that they are repelled by a magnetic field. The magnetic permeability of diamagnetic materials is slightly less than that of free space, indicating that the magnetic field is slightly weaker inside the material than in free space.

Examples of diamagnetic materials include copper, silver, gold, lead, zinc, mercury, bismuth, and graphite. These materials have no unpaired electrons in their electronic structure and are therefore diamagnetic. Water is also diamagnetic due to the presence of paired electrons in its molecular orbitals.

Diamagnetic materials have a number of practical applications, some of which include:

Magnetic levitation: Diamagnetic materials can be used to create levitating trains, which can travel at high speeds with minimal friction. This technology is currently being developed and tested in several countries.
Magnetic resonance imaging (MRI): In medical imaging, MRI uses strong magnetic fields to produce detailed images of the body. Diamagnetic materials are important for the construction of the MRI machine and for the contrast agents used to improve image quality.
Superconductivity: Many superconducting materials are diamagnetic. Superconductors are used in a wide range of applications, including electrical power transmission and medical equipment.
Electromagnetic shielding: Diamagnetic materials can be used to shield electronic devices from electromagnetic interference. This is important in a variety of applications, from sensitive laboratory equipment to consumer electronics.

Paramagnetism

Paramagnetism is a type of magnetism that arises from the presence of unpaired electrons in atoms, ions, or molecules. These unpaired electrons create tiny magnetic fields that are randomly oriented and cancel each other out, resulting in no net magnetic moment for the material in the absence of an external magnetic field.

However, when a magnetic field is applied, the magnetic fields of the unpaired electrons align with the external field, causing the material to become weakly magnetized. This effect is reversible, meaning that the material loses its magnetism when the external field is removed.

In paramagnetic materials, the magnetic susceptibility is positive, indicating that the material is weakly attracted to a magnetic field. The magnetic permeability of paramagnetic materials is slightly greater than that of free space, indicating that the magnetic field is slightly stronger inside the material than in free space.

The relative permeability of a paramagnetic material is slightly greater than 1, indicating that the material is only weakly magnetic.

Examples of paramagnetic materials include oxygen, aluminum, platinum, and titanium. These materials are weakly attracted to a magnetic field and exhibit no permanent magnetism. Other examples of paramagnetic materials include gadolinium and dysprosium, which are used in magnetic refrigeration and MRI machines due to their strong magnetic properties.

Paramagnetism is an important concept in many areas of science and technology, including the study of magnetic materials, the design of magnetic devices such as MRI machines, and materials testing and quality control. It is also used in chemical analysis, as certain compounds exhibit paramagnetic properties that can be measured to identify and quantify the presence of certain elements or compounds.

Ferromagnetism

Ferromagnetism is a type of magnetism in which certain materials become strongly magnetized in the presence of an external magnetic field.

Unlike diamagnetic and paramagnetic materials that are weakly or only temporarily magnetic, ferromagnetic materials are strongly magnetic even in the absence of an external magnetic field. This unique property of ferromagnetic materials arises from the presence of magnetic domains within the material.

Magnetic domains are regions in which the magnetic moments of the atoms are aligned in the same direction, resulting in a net magnetic moment for the domain. These domains can be thought of as tiny magnets within the material, each with its own north and south pole. In an unmagnetized ferromagnetic material, these magnetic domains are randomly oriented, resulting in a net magnetic moment of zero. However, when a strong magnetic field is applied to the material, the domains align themselves with the direction of the field, resulting in a net magnetization of the material.

As the external magnetic field is increased, more and more domains align with the field, causing the material to become magnetized. Once the material is magnetized, the domains remain aligned even after the external field is removed, resulting in a permanent magnet.

Iron, nickel, cobalt, alnico, ferrite, gadolinium, and permalloy are all examples of ferromagnetic materials used in a variety of applications including electric motors, generators, transformers, permanent magnets, magnetic recording media, and medical imaging.

Comparison between magnetic materials

Table below gives major differences between diamagnetic, paramagnetic, and ferromagnetic materials.

Diamagnetism	Paramagnetism	Ferromagnetism
Diamagnetism refers to the property of certain materials to be repelled by a magnetic field.	Paramagnetism refers to the property of certain materials to be weakly attracted by a magnetic field.	Ferromagnetism refers to the property of certain materials to become strongly magnetized in the presence of an applied magnetic field.
Diamagnetic materials have paired electrons with no net magnetic moment and are slightly repelled by magnetic fields.	Paramagnetic materials have unpaired electrons with a net magnetic moment that aligns with an applied magnetic field.	Ferromagnetic materials have unpaired electrons with a net magnetic moment that can become aligned with each other to create magnetic domains.
Arises due to paired electrons, which have no net magnetic moment and are slightly repelled by a magnetic field.	Arises due to unpaired electrons, which have a net magnetic moment that can align with an applied magnetic field to create weak attraction.	Arises due to unpaired electrons, which can align with neighboring electrons to create magnetic domains that result in strong magnetization when an external magnetic field is applied.
Diamagnetic materials have a negative susceptibility, meaning that they are slightly repelled by a magnetic field and become less magnetized in its presence	Paramagnetic materials have a positive susceptibility, meaning that they are weakly attracted to a magnetic field and become slightly more magnetized in its presence.	Ferromagnetic materials have a very high positive susceptibility, meaning that they are strongly attracted to a magnetic field and can become highly magnetized, often retaining their magnetization even after the magnetic field is removed.
Relative Permeability, $\mu_r < 1$ (less than vacuum permeability)	Relative Permeability, $\mu_r > 1$ (greater than vacuum permeability)	Relative Permeability, $\mu_r >> 1$ (much greater than vacuum permeability)
Copper, gold, silver	Aluminum, Platinum, Oxygen	Iron, Nickel, Cobalt, Gadolinium, Dysprosium