PHT110

Interference of Light

Interference of light refers to the phenomenon where two or more light waves interact with each other, resulting in a new wave pattern.

Huygens' Wave Theory

Huygens' wave theory states that every point on a wavefront can be considered as a secondary wave source, and the new wavefront is the envelope of all these secondary wavelets.

Superposition Principle

The superposition principle states that when two or more waves meet at a point, the displacement at that point is the vector sum of the displacements of the individual waves.

The mathematical equation representing the superposition principle is given by:

$$Y = y_1 + y_2$$

where y1 & y2 are displacement of individual waves and Y is the displacement of resultant wave.

Interference - Interactive simulation

Explanation of interference

Coherence

Inorder to form an interference pattern, light waves which causing it should be coherent. The conditions of coherence are,

The waves should have same wavelength or frequency
The waves should have nearly same amplitude
Two waves should have zero or a constant phase difference

Path difference and Phase difference

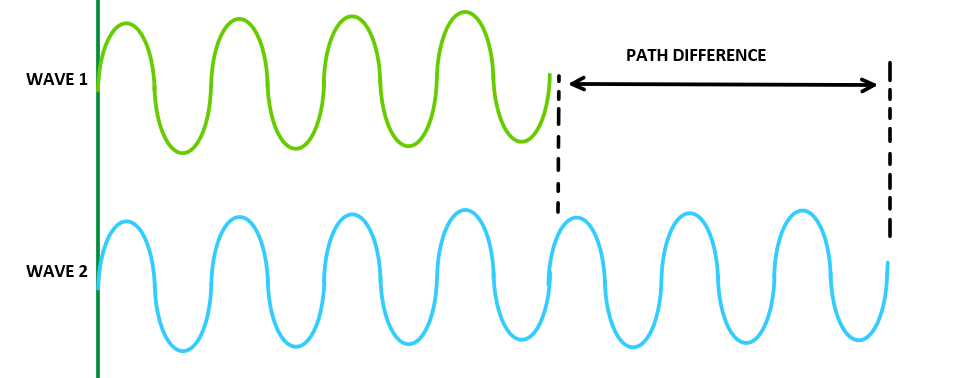
Path difference

The path difference between two waves is the difference in the distance traveled by the two waves from their point of origin to a given point in space.

Phase difference

The phase difference between two waves refers to the difference in the position of the oscillations of the two waves at a given point in time. It is measured in degrees or radians.

If the oscillations of two waves are in phase, they will have a phase difference of 0 degrees or 0 radians. If the oscillations of two waves are exactly out of phase, they will have a phase difference of 180 degrees or pi radians.

Relation between path difference and phase difference

Relation between path & phase difference

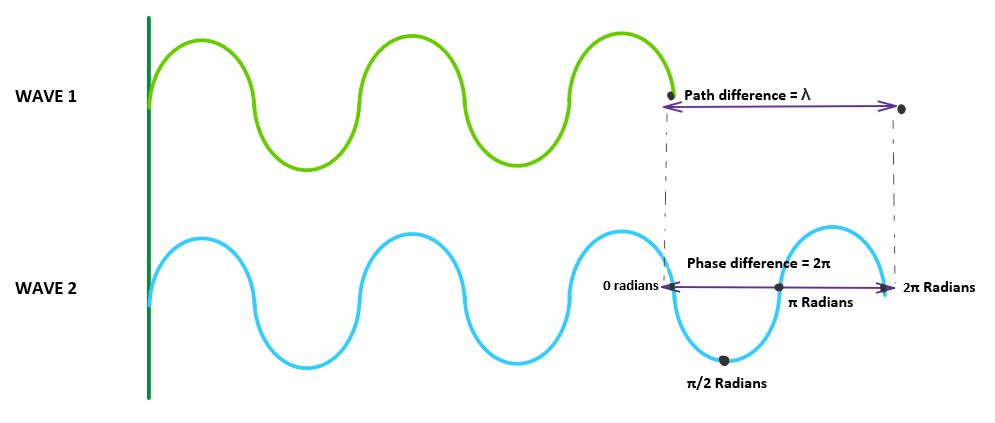
$ 2\pi $ phase difference between two waves refers to path difference of $ \lambda $ ( one wavelength ). In other hand, path difference ($\Delta x $) can be related to phase difference $ \Delta \phi $ as,

$$\boxed{ \Delta \phi = \frac{2 \pi}{\lambda}\;\Delta x} $$

Path & Phase difference illustration.

Concept of phase & phase difference.

Types of interference

Constructive Interference

If two waves interfere and gives a maximum, this type of interference is called constructive interference. The condition for maximum is that path difference between them should be an integer multiple of wavelength of light.

Condition for maximum

$$\boxed{Path\;difference=n \lambda }$$ In term of phase difference, $$Phase\;difference=2n\pi $$ where n = 1,2,3... and $ \lambda $ is the wavelength of light.

Destructive Interference

If two waves interfere and gives a minimum or darkness, this type of interference is called destructive interference. The condition for minimum is that path difference between them should be half integer multiple of wavelength of light.

Condition for minimum

$$\boxed{ Path\;difference=(2n-1) \frac{\lambda}{2} }$$ In term of phase difference, $$ Phase\;difference=(2n-1){\pi} $$ where n = 1,2,3... and $ \lambda $ is the wavelength of light.

Optical path length

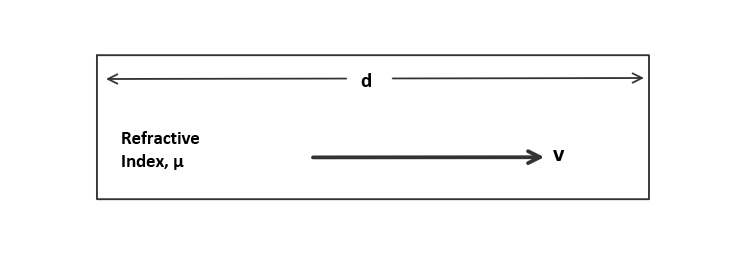
Optical path length (OPL) is a term used in optics to describe the distance that a light beam travels through a medium. It is the product of the physical distance traveled by the light ($d$) and the refractive index of the medium ( $ \mu $)through which the light is traveling.

Assume light wave get passed through a medium of width $d$. If the velocity of light through this medium is $v$ and refractive index is $\mu$, time needed to cover distance d is given by, $$t=\frac{d}{v}$$ Since optical path length (opl) is the distance light wave would travel in vaccum in same time, $ t$, $$ opl= t \times c = \frac{d}{v} \times c = d \times \frac{c}{v}=d \times \mu $$ where $ c$ is velocity of light in vaccum. So optical path length is given by, $$\boxed{ opl = \mu\;d }$$ where $ d $ is the distance travelled by light in medium of refractive index $ \mu $.

Path difference due to dissimilar reflection

When a light wave gets reflected from a denser boundary an additional path difference of λ/2 will be assigned to it.In other hand, reflection on a denser medium reverses the phase of wave by π radians.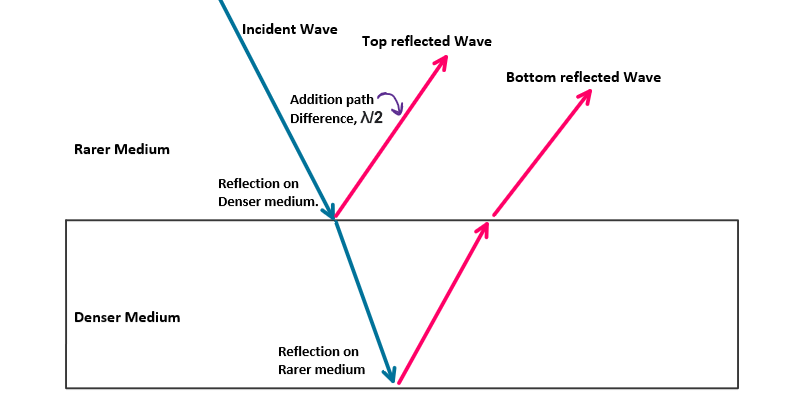

Top reflected wave gets an additional path difference λ/2 because it is reflected from boundary of denser medium.

Thin Film Interference

Thin film interference occurs when light reflects off the top and bottom surfaces of a thin film, resulting in constructive and destructive interference.

Light waves gets reflected from top and bottom surfaces. These reflected waves interferes and give alternative dark and bright bands above the film.

The condition for maximum or minimum of interference of these reflected waves depends on path difference between them. If the thickness of film is d, then path difference between reflected waves ( on from top surface and other from bottom surface ) is given by, $$pd = (BC+CD)\;in\;film - BE\;in\;air $$ So optical path difference is given by (refractive index of film is $ \mu $), $$\boxed{opd=(BC+CD)\;\mu-BE}\;-->eqn(1)$$ In △BGC, $$cos\;r=\frac{GC}{BC}=\frac{t}{BC}$$ That gives, $$BC=\frac{t}{cos\;r}$$ Since △BGC and △GCD are similar triangles, $$BC = CD $$ That gives, $$BC+CD = 2\;BC=2 \times \frac{t}{cos\;r} $$ or $$\boxed{BC+CD = \frac{2t}{cos\;r}} -->eqn(2)$$ In △BDE, $$sin\;i=\frac{BE}{BD}=\frac{BE}{BG+GD}$$ Since △BGC and △GCD are similar triangles, $$BG=GD\;ie,\;\;BG+GD=2\;BG$$ or $$sin\;i=\frac{BE}{2\;BG}$$ That gives, $$\boxed{BE=2\;BG\;sin\;i}-->eqn(3)$$ In △BGC, $$tan\;r=\frac{BG}{GC}=\frac{BG}{t}$$ which gives, $$\boxed{BG=t\;tan\;r}-->eqn(4)$$ Substituting expression for BG in eqn(3), $$\boxed{BE=2\;t\;tan\;r\;sin\;i}--eqn(5)$$ Take the expression of (BC+CD) from equation (2) and expression for BE from equation (5), substitue it in expression for optical path difference in eqn(1), $$opd=(BC+CD)\;\mu-BE$$ $$opd=\Big(\frac{2t}{cos\;r}\Big)\mu-2\;t\;tan\;r\;sin\;i-->eqn(6)$$ From snell's law at top boundary, $$ \frac{sin\;i}{sin\;r}=\frac{\mu}{1}$$ Rearranging, $$sin\;i=\mu\;sin\;r $$ Since, $ tan\;r=\frac{sin\;r}{cos\;r}$ and substituting expression for $ sin\;i $ from snells law in eqn(6), $$opd=\Big(\frac{2t}{cos\;r}\Big)\mu-2\;t\times \frac{sin\;r}{cos\;r} \times \mu\;sin\;r$$ $$opd= \Big(\frac{2\mu t}{cos\;r}\Big) - \Big(\frac{2 \mu t}{cos\;r}\Big)\;sin^2\;r $$ $$opd=\Big(\frac{2\mu t}{cos\;r}\Big)\;(1-sin^2\;r)$$ $$opd=\Big(\frac{2\mu t}{cos\;r}\Big)\;(cos^2\;r)$$ $$opd= 2\mu t \;cos\;r$$ Since reflection on top surface suffers path difference due to dissimilar reflection from a denser medium, actual path difference between top and bottom reflected waves is given by, $$\boxed{opd= 2\mu t \;cos\;r+\frac{\lambda}{2}}-->eqn(7)$$

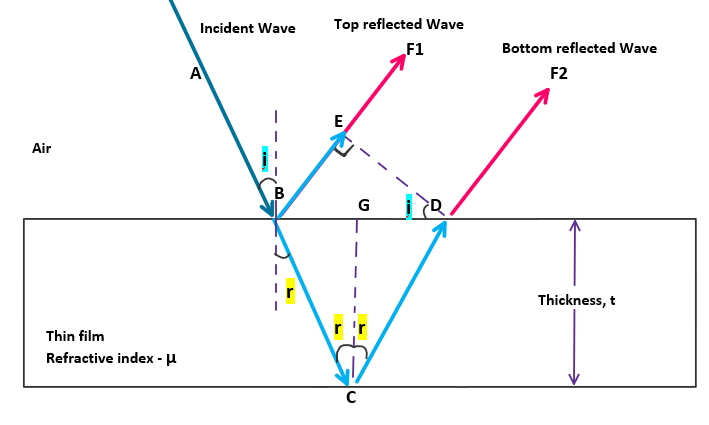
Condition for maximum

To obtain maximum at a point, optical path difference between top and bottom reflected wave should be integer multiple of wavelength. $$opd=n\;\lambda$$ Substituting expression for opd from equation(7), $$ 2\mu t \;cos\;r+\frac{\lambda}{2}=n\;\lambda $$ Rearranging, Condition for obtaining maximum on a thin film of thickness t is given by, $$\boxed{ 2\mu t \;cos\;r = (2n-1)\;\frac{\lambda}{2}}$$

Condition for minimum

To obtain minimum ordarkness at a point, optical path difference between top and bottom reflected wave should be half integer multiple of wavelength. $$opd=(2n-1)\;\frac{\lambda}{2}$$ Substituting expression for opd from equation(7), $$ 2\mu t \;cos\;r+\frac{\lambda}{2}=(2n-1)\;\frac{\lambda}{2} $$ Rearranging, Condition for obtaining maximum on a thin film of thickness t is given by, $$\boxed{ 2\mu t \;cos\;r = n\lambda}$$

Cosine law

The condition of minimum or darkness in a reflecting system or thin film is called cosine law. $$\boxed{2 \mu t \;cos\;r=n \lambda}$$ where,

$ \mu $ is the refractive index of film
$ t $ is the thickness of film
$ r $ is the angle of refraction
$ \lambda $ is wavelength of light
n = 1,2,3...

Colours in thin film

According to cosine law, light of wavelength $ \lambda $ will get cancelled or destructively interfere if the thin film obeys the condition,

$$\boxed{2 \mu t \;cos\;r=n \lambda}$$ We know that whitelight contain all the wavelengths of visible spectrum. When white light is incident on a thin film, based on thickness and angle of incidence/refraction some color ( say red) will get minimum or interfere destructively. So that part of film appears to have remaining part of white light (violet or blue).

So based on thickness variation and angle of observation, a thin film incident with white light appears colored. This effect is commonly observed in soap bubbles, peacock feathers, oil slicks, and many other natural and man-made surfaces.

Colours in soap bubbles.

Why Are Soap Bubbles So Colorful?

Air Wedge

An air wedge is a thin layer of air between two transparent surfaces, which can cause interference patterns due to the difference in refractive index.

When light passes through an air wedge, it will reflect off the top and bottom surfaces, creating constructive and destructive interference patterns. The condition of maximum and minimum are dependent on path difference between top and bottom reflected waves. For obtaining bandwidth of interference pattern, refer the figure below.

Assume that nth band forms at A where thickness of film is $ t_1 $ and (n+1)th band forms at B, where thickness is $ t_2 $.From the figure( refer △ABC ), $$tan\;\theta=\frac{t_2-t_1}{l_2-l_1}$$ Since bandwidth is defined as width of one band or distance between two adjacent bright or dark bands, we can write $l_2-l_1 = \beta $. That gives, $$tan\;\theta=\frac{t_2-t_1}{\beta}$$ Since $ \theta $ is very small, $ tan\;\theta = \theta $. That means, $$\theta=\frac{t_2-t_1}{\beta}-->eqn(1)$$ where $ \theta $ is the wedge angle and $ \beta $ is bandwidth of interference pattern. The condition for obtaining nth dark band at A with thickness $t_1$ is given by cosine law, $$2\mu t_1 cos \;r=n\lambda $$ Due to normal incidence, $r=0$ and since film is air film, $ \mu=1$: $$2\;t_1=n\lambda -->eqn(2)$$ or $$t_1=n\;\frac{\lambda}{2}$$ Similarly, condition for obtaining (n+1)th dark band at A with thickness $t_1$ is given by, $$2\mu t_2 cos \;r=(n+1)\lambda $$ or $$2t_2=(n+1)\lambda $$ which gives, $$ t_2=(n+1)\;\frac{\lambda}{2}-->eqn(3)$$ Substracting equation(2) from equation(3), $$t_2-t_1 = \frac{\lambda}{2}-->eqn(4)$$ Take equation(1) and substitute expression for $t_2-t_1 $ from equation (4); $$\theta=\frac{\lambda}{2\beta}$$ Rearranging, Bandwidth of air wedge interference pattern is given by, $$\boxed{\;\;\beta = \frac{\lambda}{2\theta}\;\;}-->eqn(5)$$

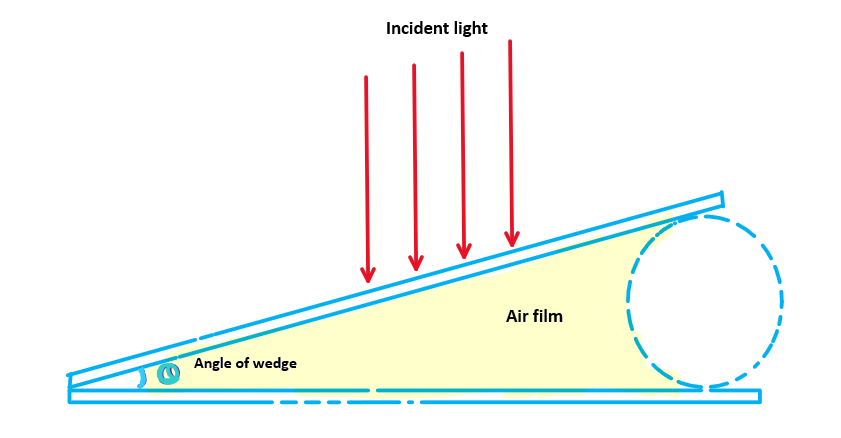
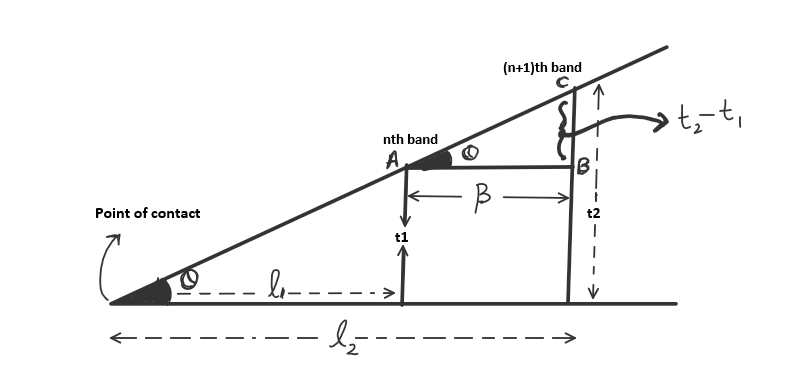
Where θ is the wedge angle and λ is the wavelength of the light used.

If a medium of refractive index $ \mu $ is filled rather than air, then bandwidth is given by, $$\boxed{\;\;\beta = \frac{\lambda}{2\;\mu\;\theta}\;\;}$$

Applications of Air wedge

Air wedge is an experimental apparatus in following applications.

Diameter of thin wire

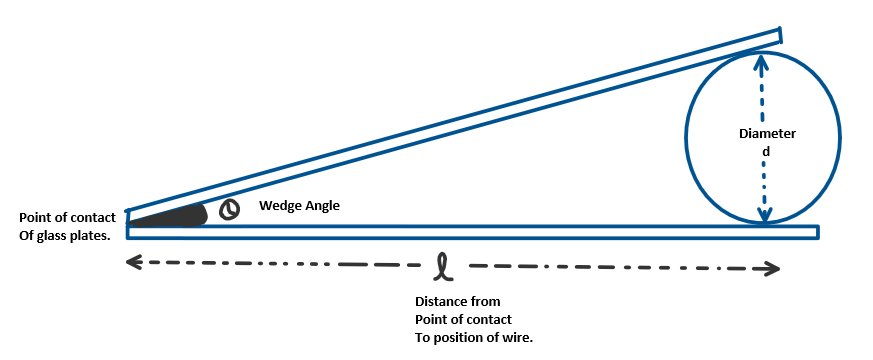
From the air wedge apparatus shown above, $$tan\;\theta=\frac{d}{l}$$ Since $ \theta $ is very small, $$ \theta = \frac{d}{l}-->eqn(6)$$ From expression for bandwidth ( refer eqn(5)), $$\beta = \frac{\lambda}{2\theta} $$ or $$\theta = \frac{\lambda}{2\beta}-->eqn(7) $$ Comparing equation(6) and (7), $$\frac{d}{l} =\frac{\lambda}{2\beta} $$ That gives diameter of thin wire placed between glass plates in air wedge as,

$$\boxed{\;\;\;d = \frac{l \lambda}{2 \beta}\;\;\;}$$

Where:

d is the thickness or diameter of the wire

λ is the wavelength of the light used

$ \beta $ is the bandwidth of interference pattern

Optical planeness of glass plates

Air wedges can also be used to check the optical planeness of a surface. By measuring the angular position of the maxima and minima, it is possible to determine the uniformity of the air gap between the surface and the transparent surface. Any variations in the thickness of the air gap will result in variations in the angular position of the maxima and minima, indicating that the surface is not optically plane.

Newton's Rings

Newton's rings are a pattern of concentric circles formed by the interference of light reflecting off the front and back surfaces of a spherical lens. The phenomenon was first observed and described by Sir Isaac Newton in his book "Opticks" in 1704.

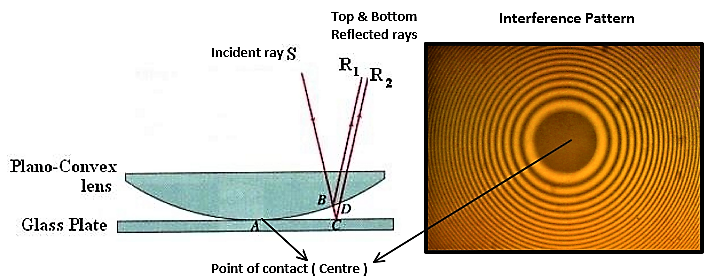
Newton's Ring apparatus and interference pattern.

When a plano-convex lens is placed on a flat surface (or glass plate) a thin air film will be formed between lens and glassplate. If this is illuminated with monochromatic light, the light reflecting from top and bottom part of this film interfere with each other. This interference will result in a pattern of bright and dark rings, with the center of the pattern being the point of contact between the lens and the flat surface.

Radius of nth dark ring

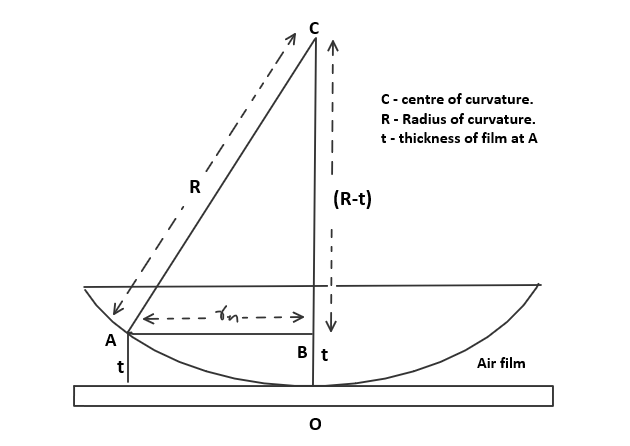
Assume that nth ring form at position A, where thickness of film is t. From figure △ABC, $$ AB^2+BC^2=AC^2$$ $$ r_n^2 + (R-t)^2 = R^2 $$ $$ r_n^2 + R^2 -2tR + t^2 = R^2$$ Since thickness t is very small, neglect the term $ t^2 $. $$r_n^2 = 2tR -->eqn(1)$$ Condition for forming nth dark ring at thickness t is given by (cosine law), $$ 2 \mu t \;cos\;r = n \lambda $$ Assume normal incidence ( r = 0 ) and air film is between lens and plate ( $ \mu = 1 $), $$2t=n\lambda -->eqn(2)$$ Substituting this value of $ 2t $ in equation(1), $$r_n^2 = 2tR = n \lambda \times R = R n \lambda $$ Hence radius of nth dark ring is given by, $$\boxed{\;\;r_n = \sqrt{Rn \lambda}\;\;}$$

Where R is the radius of curvature of the lens and λ is the wavelength of the light used.

Applications of newton's rings

Newton's rings can be used to ,

Calculation of wavelength

Radius of nth dark ring is given as, $$ r_n = \sqrt{Rn \lambda} $$ So the diameter of nth dark ring $ D_n $ is given by [ $ diameter = 2 \times radius $], $$ D_n = 2 \sqrt{Rn \lambda} $$ squaring both sides, $$D_n^2 = 4Rn \lambda -->eqn(3)$$ Diameter of (n+k)th dark ring is given by, $$D_{n+k}^2 = 4R(n+k) \lambda -->eqn(4)$$ Subracting equation(3) from equation(4), $$D_{n+k}^2 - D_n^2 = 4R(n+k) \lambda - 4Rn \lambda $$ $$D_{n+k}^2 - D_n^2 = 4Rk \lambda-->eqn(5)$$ Or wavelength can be calculated as, $$\boxed{\;\lambda = \frac{D_{n+k}^2 - D_n^2}{4Rk}\;}$$

where $ D_{n+k} $ is the diameter of (n+k) th ring and $ D_{n} $ is diameter of nth dark ring. R is the radius of curvature of lens used in this experiment.

Calculation of refractive index

If the gap between plano convex lens and glass plate is filled with any liquid of refractive index $ \mu $, radius of nth dark ring can be modified as, $$r_n^2 = \frac{R n \lambda}{\mu} $$ So diameter of nth ring and (n+k)th ring will be , $$d_n^2 = \frac{4Rn \lambda}{\mu}$$ $$d_{n+k}^2 = \frac{4R(n+k) \lambda}{\mu}$$ Subracting each other, $$d_{n+k}^2 - d_n^2 = \frac{4Rk \lambda}{\mu} -->eqn(6)$$ Dividing equation(5) with equation(6), We get the refractive index of liquid as, $$\boxed{\;\mu = \frac{D_{n+k}^2 - D_n^2}{d_{n+k}^2 - d_n^2}\;}$$ where $D_n $ and $ D_{n+k} $ are diameters of nth and (n+k)th dark ring when air is between glass plate and lens. $ d_n $ and $ d_{n+k} $ are diameters of nth and (n+k)th dark rings when liquid of refractive index $ \mu $ is introduced between lens and plate.

Anti-Reflection Coating

Anti-reflection coatings are thin films applied to surfaces to reduce the amount of reflection that occurs. They work by introducing a thin layer of material with a lower refractive index than the surface it is applied to. This creates a difference in the phase of the light waves reflecting off the surface and the coating, which results in constructive and destructive interference, reducing the overall amount of reflected light.

Anti-reflection coatings are commonly used on lenses, mirrors, and other optical surfaces to improve transmission and reduce glare.

Interference Filters

Interference filters are optical devices that use the principle of constructive and destructive interference to selectively pass certain wavelengths of light while blocking others. They consist of multiple thin film layers with varying refractive indices, which cause the different wavelengths of light to experience different amounts of phase shift, resulting in selective transmission or reflection.

Interference filters are used in a variety of applications, including spectroscopy, imaging, and color separation.

What is Anti Reflective Coating?

Thin film and light.

Numerical questions for Assignment

( Each question contains 3 marks )

Enter your roll number