Fibre Optics
Total internal reflection
Total internal reflection is a phenomenon where light is reflected back into a denser medium it came from, when angle of incidence is greater than a limiting angle called critical angle..
The figure below illustrates total internal reflection when angle of incidence is greater than critical angle.

Optical fibre - Structure
An optical fibre is contains inner cylindrical core with higher refractive index ( say n1 ). Surrounding the core, there is a part called cladding with lower refractive index ( say n2 ).
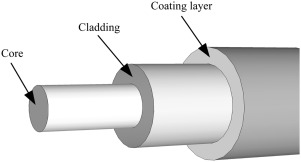
There exists a sheath or protective covering enclosing core and cladding which ensures safety of fibre. Light is transmitted through the fibre via total internal reflection.
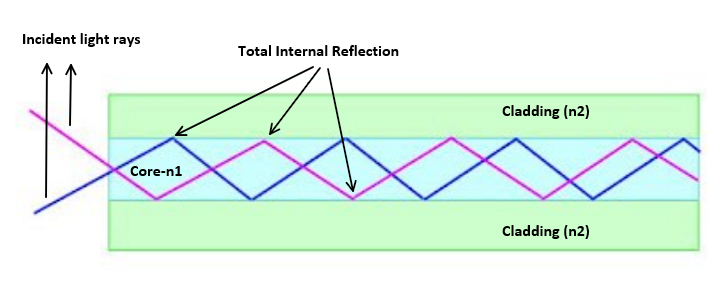
Propagation of light in fibre
Light rays get propagated through fibre by multiple total internal reflections at core-cladding boundary.
Acceptance angle
The acceptance angle of an optical fiber is the maximum angle at which light can enter the fiber and still be efficiently guided along its length. The light rays with angle of incidence less than acceptance angle only get propagated through fibre via total internal reflection.
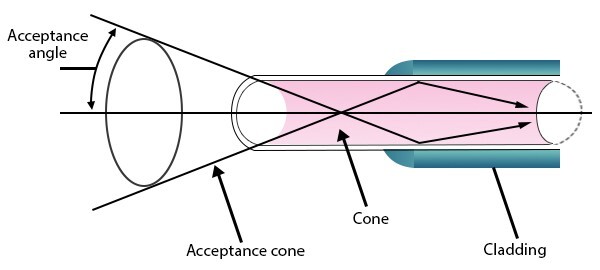
Acceptance Cone
The acceptance cone is the cone-shaped region in which light can enter the fiber and be guided efficiently. This is the three dimensional aspect of acceptance angle. Those light rays which falls inside acceptance cone can only get propagated through fibre.
Think of it like a cone-shaped bucket that an optical fiber uses to gather light. The bigger the cone, the more light it can collect.
Numerical Aperture (NA)
Numerical aperture (NA) is a measure of how much light an optical fiber can collect and transmit. It is the sine function of acceptance angle.
$$NA = sin\;\theta_a $$ where \( \theta_a \) is the acceptance angle.Numerical aperture can be also be defined in terms of refractive indices of core and cladding as,
$$NA = \sqrt{n_1^2-n_2^2}$$ where \( n_1 \) is refractive index of core and \( n_2 \) is of cladding.Derivation of expression for NA
Define NA as the sine of the acceptance angle \(\alpha\), i.e. $$NA = \sin(\alpha)$$ Consider an optical fiber with a core of refractive index $n_1$ and cladding of refractive index $n_2$.
By Snell's law, we have: $$\frac{sin\;\alpha}{sin\;\theta}=\frac{n_1}{\mu}$$ where $\theta$ is the angle of refraction or angle that the ray makes with the normal to the fiber axis inside the cladding.
Rearranging above expression,
Substituting $\theta_{max}$ into the expression for NA, we get: $$NA = n_1 \sin(\theta_{max}) = n_1 \frac{n_2}{n_1} = \sqrt{n_1^2 - n_2^2}$$ Therefore, the final expression for numerical aperture in an optical fiber is $$NA = \sqrt{n_1^2 - n_2^2}$$ where $n_1$ is the refractive index of the core and $n_2$ is the refractive index of the cladding.Step-Index fibre
A step-index fibre is a type of optical fibre where the refractive index of the core is constant, and the refractive index of the cladding is different.
This type of fibre has a lower numerical aperture and a lower bandwidth compared to graded-index fibres.
Graded-Index fibre
A graded-index fibre is a type of optical fibre where the refractive index of the core is not constant, but varies in a specific way.
This type of fibre has a higher numerical aperture and a higher bandwidth compared to step-index fibres. This allows for a larger acceptance angle and reduces modal dispersion, leading to improved signal transmission over longer distances.
Fibre optic communication system
A fibre optic communication system uses optical fibres to transmit information over long distances.
It is a highly efficient and reliable form of communication, with a wide range of applications including telecommunications, internet connectivity, and medical imaging.
Applications of optical fibres
Optical fibres are used in a wide range of applications including telecommunications, internet connectivity, medical imaging, and industrial sensing.
They are also used in scientific research, such as in spectroscopy and interferometry.
Numerical problems
This section provides some sample numerical problems related to fibre optics.
These problems may include calculations related to refractive index, numerical aperture, and light transmission through optical fibres.